Kondensator

Was ist Kondensator und Kondensator Berechnungen.

Was ist Kondensator?

Der Kondensator ist eine elektronische Komponente, die elektrische Ladung speichert . Der Kondensator besteht aus 2 engen Leitern (normalerweise Platten), die durch ein dielektrisches Material getrennt sind. Die Platten sammeln elektrische Ladung, wenn sie an eine Stromquelle angeschlossen werden. Eine Platte sammelt positive Ladung und die andere Platte akkumuliert negative Ladung.

Die Kapazität ist die Menge an elektrischer Ladung, die bei einer Spannung von 1 Volt im Kondensator gespeichert ist.

Die Kapazität wird in Einheiten von Farad (F) gemessen .

Der Kondensator trennt den Strom in Gleichstromkreisen und den Kurzschluss in Wechselstromkreisen.

Kondensatorbilder

Kondensatorsymbole

Kondensator
Polarisierter Kondensator
Variabler Kondensator
  

Kapazität

Die Kapazität (C) des Kondensators ist gleich der elektrischen Ladung (Q) geteilt durch die Spannung (V):

C = \ frac {Q} {V}

C ist die Kapazität in Farad (F)

Q ist die elektrische Ladung in Coulomb (C), die auf dem Kondensator gespeichert ist

V ist die Spannung zwischen den Platten des Kondensators in Volt (V)

Kapazität des Plattenkondensators

Die Kapazität (C) des Plattenkondensators ist gleich der Permittivität (ε) mal der Plattenfläche (A) geteilt durch den Spalt oder Abstand zwischen den Platten (d):

 

C = \ varepsilon \ times \ frac {A} {d}

C ist die Kapazität des Kondensators in Farad (F).

ε ist die Permittivität des dialektischen Materials des Kondensators in Farad pro Meter (F / m).

A ist die Fläche der Kondensatorplatte in Quadratmetern (m 2 ].

d ist der Abstand zwischen den Platten des Kondensators in Metern (m).

Kondensatoren in Reihe

 

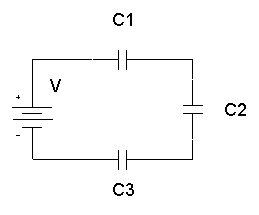
Die Gesamtkapazität der Kondensatoren in Reihe, C1, C2, C3, ..:

\ frac {1} {C_ {Total}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} {C_ {3}} + .. .

Kondensatoren parallel

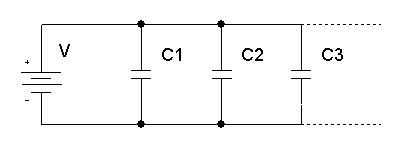
Die Gesamtkapazität der parallelen Kondensatoren, C1, C2, C3, ..:

C Gesamt = C 1 + C 2 + C 3 + ...

Kondensatorstrom

Der momentane Strom des Kondensators i c (t) ist gleich der Kapazität des Kondensators.

mal die Ableitung der Spannung des Momentkondensators v c (t):

i_c (t) = C \ frac {dv_c (t)} {dt}

Kondensatorspannung

Die Momentanspannung v c (t) des Kondensators ist gleich der Anfangsspannung des Kondensators.

plus 1 / C-faches Integral des Stroms des Momentkondensators i c (t) über die Zeit t:

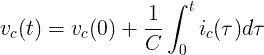
v_c (t) = v_c (0) + \ frac {1} {C} \ int_ {0} ^ {t} i_c (\ tau) d \ tau

Energie des Kondensators

Die gespeicherte Energie E C des Kondensators in Joule (J) ist gleich der Kapazität C in Farad (F)

mal die Spannung V C des quadratischen Kondensators in Volt (V) geteilt durch 2:

E C = C × V C 2 /2

Wechselstromkreise

Winkelfrequenz

ω = 2 π f

ω - Winkelgeschwindigkeit gemessen im Bogenmaß pro Sekunde (rad / s)

f - Frequenz gemessen in Hertz (Hz).

Kondensatorreaktanz

X_C = - \ frac {1} {\ omega C}

Kondensatorimpedanz

Kartesische Form:

Z_C = jX_C = -j \ frac {1} {\ omega C}

Polare Form:

Z C = X C ∟-90º

Kondensatortypen

Variabler Kondensator Der variable Kondensator hat eine veränderbare Kapazität
Elektrolytkondensator Elektrolytkondensatoren werden verwendet, wenn eine hohe Kapazität benötigt wird. Die meisten Elektrolytkondensatoren sind polarisiert
Kugelkondensator Der Kugelkondensator hat eine Kugelform
Leistungskondensator Leistungskondensatoren werden in Hochspannungsversorgungssystemen verwendet.
Keramikkondensator Keramikkondensator hat keramisches dielektrisches Material. Hat Hochspannungsfunktionalität.
Tantalkondensator Dielektrisches Tantaloxidmaterial. Hat eine hohe Kapazität
Glimmerkondensator Hochgenaue Kondensatoren
Papierkondensator Dielektrisches Papiermaterial

 

Siehe auch:

ELEKTRONISCHE BAUTEILE
SCHNELLE TABELLEN