Kondensators

Kas ir kondensatora un kondensatora aprēķini.

Kas ir kondensators

Kondensators ir elektroniska sastāvdaļa, kas uzglabā elektrisko lādiņu . Kondensators ir izgatavots no 2 tuviem vadītājiem (parasti plāksnēm), kurus atdala dielektrisks materiāls. Plātnes uzkrāj elektrisko lādiņu, kad tās ir savienotas ar barošanas avotu. Viena plāksne uzkrāj pozitīvo lādiņu, bet otra - negatīvo.

Kapacitāte ir elektriskā lādiņa daudzums, kas tiek uzglabāts kondensatorā pie 1 voltu sprieguma.

Kapacitāti mēra Farada (F) vienībās .

Kondensators atvieno strāvu līdzstrāvas (DC) ķēdēs un īssavienojumu maiņstrāvas (AC) ķēdēs.

Kondensatora attēli

Kondensatora simboli

Kondensators
Polarizēts kondensators
Maināms kondensators
  

Kapacitāte

Kondensatora kapacitāte (C) ir vienāda ar elektrisko lādiņu (Q), dalītu ar spriegumu (V):

C = \ frac {Q} {V}

C ir kapacitāte faradā (F)

Q ir elektriskais lādiņš kulonos (C), kas tiek uzglabāts kondensatorā

V ir spriegums starp kondensatora plāksnēm voltos (V)

Plākšņu kondensatora kapacitāte

Plākšņu kondensatora kapacitāte (C) ir vienāda ar caurlaidību (ε), kas reizināts ar plāksnes laukumu (A), dalītu ar atstarpi vai attālumu starp plāksnēm (d):

 

C = \ varepsilon \ times \ frac {A} {d}

C ir kondensatora kapacitāte faradā (F).

ε ir kondensatora dialektiskā materiāla caurlaidība farādos uz metru (F / m).

A ir kondensatora plāksnes laukums kvadrātmetros (m 2 ].

d ir attālums starp kondensatora plāksnēm metros (m).

Kondensatori virknē

 

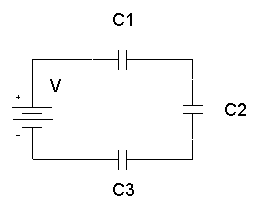
Kondensatoru sērijveida kopējā kapacitāte, C1, C2, C3, ..:

\ frac {1} {C_ {Total}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} {C_ {3}} + .. .

Kondensatori paralēli

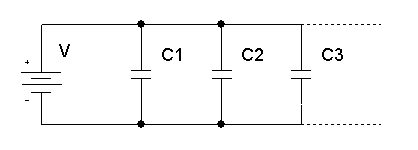
Kondensatoru kopējā kapacitāte paralēli, C1, C2, C3, ..:

C Kopā = C 1 + C 2 + C 3 + ...

Kondensatora strāva

Kondensatora momentālā strāva i c (t) ir vienāda ar kondensatora kapacitāti,

reizina momentāna kondensatora sprieguma v c (t) atvasinājumu :

i_c (t) = C \ frac {dv_c (t)} {dt}

Kondensatora spriegums

Kondensatora momentālais spriegums v c (t) ir vienāds ar kondensatora sākotnējo spriegumu,

plus 1 / C reizes lielāks par momentānās kondensatora strāvas i c (t) integrālu laika gaitā t:

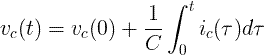
v_c (t) = v_c (0) + \ frac {1} {C} \ int_ {0} ^ {t} i_c (\ tau) d \ tau

Kondensatora enerģija

Kondensatora uzkrātā enerģija E C džoulos (J) ir vienāda ar kapacitāti C faradā (F)

reizina kvadrātveida kondensatora spriegumu V C voltos (V), dalot ar 2:

E C = C × V C 2 /2

Maiņstrāvas ķēdes

Leņķiskā frekvence

ω = 2 π f

ω - leņķiskais ātrums, ko mēra radiānos sekundē (rad / s)

f - frekvence, kas mērīta hercos (Hz).

Kondensatora reaktivitāte

X_C = - \ frac {1} {\ omega C}

Kondensatora pretestība

Dekarta forma:

Z_C = jX_C = -j \ frac {1} {\ omega C}

Polārā forma:

Z C = X C ∟ -90º

Kondensatoru veidi

Maināms kondensators Mainīgajam kondensatoram ir maināma kapacitāte
Elektrolītiskais kondensators Elektrolītiskos kondensatorus izmanto, ja nepieciešama liela kapacitāte. Lielākā daļa elektrolītisko kondensatoru ir polarizēti
Sfērisks kondensators Sfēriskajam kondensatoram ir sfēras forma
Jaudas kondensators Jaudas kondensatori tiek izmantoti augstsprieguma energosistēmās.
Keramikas kondensators Keramikas kondensatoram ir keramikas dielektriskais materiāls. Ir augstsprieguma funkcionalitāte.
Tantala kondensators Tantala oksīda dielektriskais materiāls. Ir augsta kapacitāte
Vizlas kondensators Augstas precizitātes kondensatori
Papīra kondensators Papīra dielektriskais materiāls

 

Skatīt arī:

ELEKTRONISKĀS SASTĀVDAĻAS
ĀTRAS TABULAS