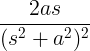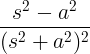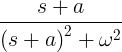ലാപ്ലേസ് പരിവർത്തനം
- ലാപ്ലേസ് ട്രാൻസ്ഫോർം ഫംഗ്ഷൻ
- ലാപ്ലേസ് പരിവർത്തന പട്ടിക
- ലാപ്ലേസ് പരിവർത്തന സവിശേഷതകൾ
- ലാപ്ലേസ് പരിവർത്തന ഉദാഹരണങ്ങൾ
ലാപ്ലേസ് പരിവർത്തനം പൂജ്യത്തിൽ നിന്ന് അനന്തതയിലേക്ക് സംയോജിപ്പിച്ച് ഒരു സമയ ഡൊമെയ്ൻ പ്രവർത്തനത്തെ എസ്-ഡൊമെയ്ൻ പ്രവർത്തനത്തിലേക്ക് പരിവർത്തനം ചെയ്യുന്നു
ടൈം ഡൊമെയ്ൻ ഫംഗ്ഷന്റെ, e -st കൊണ്ട് ഗുണിച്ചാൽ .
ഡിഫറൻഷ്യൽ സമവാക്യങ്ങൾക്കും ഇന്റഗ്രലുകൾക്കും വേഗത്തിൽ പരിഹാരം കണ്ടെത്തുന്നതിന് ലാപ്ലേസ് പരിവർത്തനം ഉപയോഗിക്കുന്നു.
ടൈം ഡൊമെയ്നിലെ വ്യുൽപ്പന്നം s- ഡൊമെയ്നിലെ s കൊണ്ട് ഗുണനത്തിലേക്ക് പരിവർത്തനം ചെയ്യുന്നു.
ടൈം ഡൊമെയ്നിലെ സംയോജനം s- ഡൊമെയ്നിലെ s കൊണ്ട് ഹരണങ്ങളായി പരിവർത്തനം ചെയ്യുന്നു.
ലാപ്ലേസ് ട്രാൻസ്ഫോർം ഫംഗ്ഷൻ
L }} ഓപ്പറേറ്റർ ഉപയോഗിച്ച് ലാപ്ലേസ് പരിവർത്തനം നിർവചിച്ചിരിക്കുന്നു :
![]()
വിപരീത ലാപ്ലേസ് പരിവർത്തനം
വിപരീത ലാപ്ലേസ് പരിവർത്തനം നേരിട്ട് കണക്കാക്കാം.
സാധാരണയായി വിപരീത പരിവർത്തനം പരിവർത്തന പട്ടികയിൽ നിന്ന് നൽകുന്നു.
ലാപ്ലേസ് പരിവർത്തന പട്ടിക
| പ്രവർത്തനത്തിന്റെ പേര് | സമയ ഡൊമെയ്ൻ പ്രവർത്തനം | ലാപ്ലേസ് പരിവർത്തനം |
|---|---|---|
f ( ടി ) |
F ( കൾ ) = L { f ( t )} |
|
| നിരന്തരമായ | 1 | |
| ലീനിയർ | t | |
| പവർ | t n |
|
| പവർ | t a |
Γ ( ഒരു +1 ചെയ്യുക) ⋅ ന്റെ - ( ഒരു +1 ചെയ്യുക) |
| എക്സ്പോണന്റ് | e at |
|
| സൈൻ | പാപം ചെയ്തത് |
|
| കോസിൻ | cos at |
|
| ഹൈപ്പർബോളിക് സൈൻ | at sinh |
|
| ഹൈപ്പർബോളിക് കോസൈൻ | at cosh |
|
| വളരുന്ന സൈൻ | ടി പാപം ചെയ്തത് |
|
| വളരുന്ന കോസൈൻ | ടി കോസ് ചെയ്തത് |
|
| ക്ഷയിക്കുന്നു | e -at sin ωt |
|
| അഴുകുന്ന കോസൈൻ | e -at cos ωt |
|
| ഡെൽറ്റ പ്രവർത്തനം | T ( ടി ) |
1 |
| ഡെൽറ്റ വൈകി | δ ( ടാ ) |
e -as |
ലാപ്ലേസ് പരിവർത്തന സവിശേഷതകൾ
| സ്വത്തിന്റെ പേര് | സമയ ഡൊമെയ്ൻ പ്രവർത്തനം | ലാപ്ലേസ് പരിവർത്തനം | അഭിപ്രായം |
|---|---|---|---|
f ( ടി ) |
എഫ് ( കൾ ) |
||
| ലീനിയറിറ്റി | af ( t ) + bg ( t ) | aF ( കൾ ) + ബിജി ( കൾ ) | a , b സ്ഥിരമാണ് |
| സ്കെയിൽ മാറ്റം | f ( at ) | |
a / 0 |
| ഷിഫ്റ്റ് | e -at f ( t ) | F ( s + a ) | |
| കാലതാമസം | f ( ta ) | ഇ - പോലെ എഫ് ( ങ്ങൾ ) | |
| വ്യുൽപ്പന്നം | |
sF ( കൾ ) - f (0) | |
| N-th ഡെറിവേഷൻ | |
s n f ( കൾ ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0) | |
| പവർ | t n f ( t ) | |
|
| സംയോജനം | |
|
|
| പരസ്പരവിരുദ്ധം | |
|
|
| പരിവർത്തനം | f ( t ) * g ( t ) | F ( കൾ ) ⋅ G ( കൾ ) | * ആണ് കൺവോൾഷൻ ഓപ്പറേറ്റർ |
| ആനുകാലിക പ്രവർത്തനം | f ( t ) = f ( t + T ) | |
ലാപ്ലേസ് പരിവർത്തന ഉദാഹരണങ്ങൾ
ഉദാഹരണം # 1
F (t) ന്റെ പരിവർത്തനം കണ്ടെത്തുക:
f ( t ) = 3 t + 2 t 2
പരിഹാരം:
ℒ { t } = 1 / സെ 2
ℒ { t 2 } = 2 / സെ 3
F ( കൾ ) = ℒ { f ( t )} = ℒ t 3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3
ഉദാഹരണം # 2
എഫ് (കൾ) ന്റെ വിപരീത പരിവർത്തനം കണ്ടെത്തുക:
F ( കൾ ) = 3 / ( s 2 + s - 6)
പരിഹാരം:
വിപരീത പരിവർത്തനം കണ്ടെത്തുന്നതിന്, ഞങ്ങൾ ഡൊമെയ്ൻ പ്രവർത്തനം ലളിതമായ രൂപത്തിലേക്ക് മാറ്റേണ്ടതുണ്ട്:
F ( കൾ ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)
[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]
a ( s +3) + b ( s -2) = 3
A, b എന്നിവ കണ്ടെത്തുന്നതിന്, നമുക്ക് 2 സമവാക്യങ്ങൾ ലഭിക്കുന്നു - s ന്റെ ഗുണകങ്ങളിൽ ഒന്ന്, ബാക്കിയുള്ളതിൽ രണ്ടാമത്തേത്:
( a + b ) s + 3 a -2 b = 3
a + b = 0, 3 a -2 b = 3
a = 3/5, ബി = -3/5
F ( കൾ ) = 3/5 ( s -2) - 3/5 ( s +3)
എക്സ്പോണന്റ് ഫംഗ്ഷനായി ട്രാൻസ്ഫോർംസ് പട്ടിക ഉപയോഗിച്ച് ഇപ്പോൾ എഫ് (കൾ) എളുപ്പത്തിൽ പരിവർത്തനം ചെയ്യാൻ കഴിയും:
f ( t ) = (3/5) e 2 t - (3/5) e -3 t
ഇതും കാണുക
കാൽക്കുലസ്
- പരിധി
- ഡെറിവേറ്റീവ്
- ഇന്റഗ്രൽ
- സീരീസ്
- ലാപ്ലേസ് പരിവർത്തനം
- പരിവർത്തനം
- കാൽക്കുലസ് ചിഹ്നങ്ങൾ
ദ്രുത പട്ടികകൾ