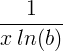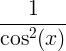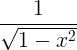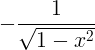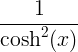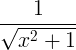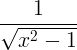Johdannaissäännöt
Johdannaissäännöt ja lait. Johdannaiset funktiotaulukosta.
Johdannaisen määritelmä
Funktion derivaatti on funktion arvon f (x) erotuksen suhde pisteissä x + Δx ja x pisteiden Δx kanssa, kun Δx on äärettömän pieni. Johdannainen on tangenttiviivan funktion kaltevuus tai kaltevuus pisteessä x.
![]()
Toinen johdannainen
Toinen johdannainen saadaan:
![]()
Tai yksinkertaisesti johtaa ensimmäinen johdannainen:
![]()
Yhdeksäs johdannainen
N : nnen johdannainen lasketaan johtamalla f (x) n kertaa.
N : nnen johdannainen on yhtä suuri kuin johdannainen (n-1) johdannainen:
f ( n ) ( x ) = [ f ( n -1) ( x )] '
Esimerkki:
Etsi neljäs johdannainen
f ( x ) = 2 x 5
f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' = [40 x 3 ] '' = [120 x 2 ] '= 240 x
Johdannainen funktion kaaviossa
Funktion derivaatti on tangentiaalisen viivan kaltevuus.
Johdannaissäännöt
| Johdannaissumman sääntö | ( af ( x ) + bg ( x )) = = af ( x ) + bg ' ( x ) |
| Johdannaistuotesääntö | ( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x ) |
| Johdannaisen osamissääntö | 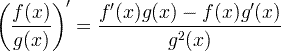 |
| Johdannainen ketjusääntö | f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x ) |
Johdannaissumman sääntö
Kun a ja b ovat vakioita.
( af ( x ) + bg ( x )) = = af ( x ) + bg ' ( x )
Esimerkki:
Etsi johdannainen:
3 x 2 + 4 x.
Summasäännön mukaan:
a = 3, b = 4
f ( x ) = x 2 , g ( x ) = x
f ' ( x ) = 2 x , g' ( x ) = 1
(3 x 2 + 4 x )'= 3⋅2 x + 4⋅1 = 6 x + 4
Johdannaistuotesääntö
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Johdannaisen osamissääntö
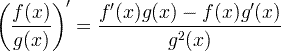
Johdannainen ketjusääntö
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )
Tämä sääntö voidaan ymmärtää paremmin Lagrangen merkinnällä:
![]()
Funktion lineaarinen likiarvo
Pienelle Δx: lle saadaan likiarvo arvoon f (x 0 + Δx), kun tiedämme f (x 0 ) ja f '(x 0 ):
f ( x 0 + Δ x ) ≈ f ( x 0 ) + f ( x 0 ) ⋅Δ x
Johdannaiset funktiotaulukosta
| Toiminnon nimi | Toiminto | Johdannainen |
|---|---|---|
| f ( x ) |
f '( x ) | |
| Jatkuva | vakio |
0 |
| Lineaarinen | x |
1 |
| Teho | x a |
kirves a- 1 |
| Eksponentiaalinen | e x |
e x |
| Eksponentiaalinen | a x |
a x ln a |
| Luonnollinen logaritmi | ln ( x ) |
|
| Logaritmi | log b ( x ) |
|
| Sini | synti x |
cos x |
| Kosini | cos x |
-sin x |
| Tangentti | rusketus x |
|
| Arcsine | arcsin x |
|
| Arkosiini | arccos x |
|
| Arkangentti | arctan x |
|
| Hyperbolinen sini | sinh x |
cosh x |
| Hyperbolinen kosini | cosh x |
sinh x |
| Hyperbolinen tangentti | tanh x |
|
| Käänteinen hyperbolinen sini | sinh -1 x |
|
| Käänteinen hyperbolinen kosini | cosh -1 x |
|
| Käänteinen hyperbolinen tangentti | tanh -1 x |
|
Johdannaisesimerkkejä
Esimerkki 1
f ( x ) = x 3 +5 x 2 + x +8
f ' ( x ) = 3 x 2 + 2 ~ 5 x + 1 + 0 = 3 x 2 +10 x +1
Esimerkki 2
f ( x ) = synti (3 x 2 )
Ketjusääntöä sovellettaessa:
f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x
Toinen johdannaistesti
Kun funktion ensimmäinen derivaatti on nolla pisteessä x 0 .
f '( x 0 ) = 0
Sitten toinen johdannainen pisteessä x 0 , f '' (x 0 ), voi osoittaa kyseisen pisteen tyypin:
| f '' ( x 0 )/ 0 |
paikallinen minimi |
| f '' ( x 0 ) <0 |
paikallinen enimmäismäärä |
| f '' ( x 0 ) = 0 |
määrittelemätön |