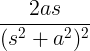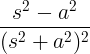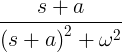Laplace-muunnos

Laplace-muunnos muuntaa aikatoiminnon funktion s-domain-funktioksi integroimalla nollasta äärettömään

^{aikatoiminnon} funktio kerrottuna e ^{-st: llä} .

Laplace-muunnosta käytetään ratkaisujen löytämiseen differentiaaliyhtälöille ja integraaleille.

Aikatoimialueen johtaminen muunnetaan kertomalla s: llä s-verkkotunnuksessa.

Aikatoimialueen integraatio muutetaan s-toimialueen s-jakoon.

Laplace-muunnostoiminto

Laplace-muunnos määritetään operaattorilla L {}:

$F (s) = \ mathcal {L} \ vasen \ {f (t) \ oikea \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

Käänteinen Laplace-muunnos voidaan laskea suoraan.

Yleensä käänteinen muunnos annetaan muunnostaulukosta.

Toiminnon nimi	Aikatoiminnon toiminto	Laplace-muunnos
Toiminnon nimi	f ( t )	F ( s ) = L { f ( t )}
Jatkuva	1	$\ frac {1} {s}$
Lineaarinen	t	$\ frac {1} {s ^ 2}$
Teho	t ⁿ	$\ frac {n!} {s ^ {n + 1}}$
Teho	t ^a	Γ ( +1) ⋅ s ^{- (}⁺¹⁾
Eksponentti	e ^klo	$\ frac {1} {sa}$
Sini	sin klo	$\ frac {a} {s ^ 2 + a ^ 2}$
Kosini	cos klo	$\ frac {s} {s ^ 2 + a ^ 2}$
Hyperbolinen sini	sinh at	$\ frac {a} {s ^ 2-a ^ 2}$
Hyperbolinen kosini	cosh at	$\ frac {s} {s ^ 2-a ^ 2}$
Kasvava sini	T sin klo	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
Kasvava kosini	t cos at	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
Rappeutuva sini	e ^-at syn ωt	$\ frac {\ omega} {\ vasen (s + a \ oikea) ^ 2 + \ omega ^ 2}$
Rappeutuva kosini	e ^-at cos ωt	$\ frac {s + a} {\ vasen (s + a \ oikea) ^ 2 + \ omega ^ 2}$
Delta-toiminto	δ ( t )	1
Viivästynyt delta	δ ( ta )	e ^-as

Kiinteistön nimi	Aikatoiminnon toiminto	Laplace-muunnos	Kommentti
	f ( t )	F ( s )
Lineaarisuus	af ( t ) + bg ( t )	aF ( s ) + bG ( s )	a , b ovat vakioita
Skaalamuutos	f ( at )	$\ frac {1} {a} F \ vasen (\ frac {s} {a} \ oikea)$	a / 0
Siirtää	e ^-at f ( t )	F ( s + a )
Viive	f ( ta )	e ^{- kuten} F ( s )
Johtaminen	$\ frac {df (t)} {dt}$	sF ( s ) - f (0)
N: s johto	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
Teho	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
Liittäminen	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F (t)$
Vastavuoroinen	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
Konvoluutio	f ( t ) * g ( t )	F ( s ) ⋅ G ( s )	* on konvoluutiooperaattori
Jaksollinen toiminta	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$