Equazione quadrata
L'equazione quadratica è un polinomio del secondo ordine con 3 coefficienti: a , b , c .
L'equazione quadratica è data da:
ax 2 + bx + c = 0
La soluzione all'equazione quadratica è data da 2 numeri x 1 ex 2 .
Possiamo cambiare l'equazione quadratica nella forma di:
( x - x 1 ) ( x - x 2 ) = 0
Formula quadratica
La soluzione all'equazione quadratica è data dalla formula quadratica:
![]()
L'espressione all'interno della radice quadrata è chiamata discriminante ed è denotata da Δ:
Δ = b 2 - 4 ac
La formula quadratica con notazione discriminante:
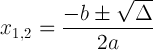
Questa espressione è importante perché può dirci la soluzione:
- Quando Δ/ 0, ci sono 2 radici reali x 1 = (- b + √ Δ ) / (2a) e x 2 = (- b-√ Δ ) / (2a) .
- Quando Δ = 0, c'è una radice x 1 = x 2 = -b / (2a) .
- Quando Δ <0, non ci sono radici reali, ci sono 2 radici complesse:
x 1 = (- b + i√ -Δ ) / (2a) e x 2 = (- bi√ -Δ ) / (2a) .
Problema n. 1
3 x 2 +5 x +2 = 0
soluzione:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Problema n. 2
3 x 2 -6 x 3 = 0
soluzione:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Problema n. 3
x 2 +2 x +5 = 0
soluzione:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Non ci sono soluzioni reali. I valori sono numeri complessi:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Grafico delle funzioni quadratiche
La funzione quadratica è una funzione polinomiale del secondo ordine:
f ( x ) = ax 2 + bx + c
Le soluzioni dell'equazione quadratica sono le radici della funzione quadratica, che sono i punti di intersezione del grafico della funzione quadratica con l'asse x, quando
f ( x ) = 0
Quando ci sono 2 punti di intersezione del grafico con l'asse x, ci sono 2 soluzioni per l'equazione quadratica.
Quando c'è 1 punto di intersezione del grafico con l'asse x, c'è 1 soluzione per l'equazione quadratica.
Quando non ci sono punti di intersezione del grafico con l'asse x, otteniamo soluzioni non reali (o 2 soluzioni complesse).