Regole logaritmiche
Il logaritmo in base b di un numero è l' esponente di cui abbiamo bisogno per aumentare la base per ottenere il numero.
- Definizione logaritmo
- Regole logaritmiche
- Problemi di logaritmo
- Logaritmo complesso
- Grafico del log (x)
- Tabella dei logaritmi
- Calcolatrice logaritmo
Definizione logaritmo
Quando b è elevato alla potenza di y è uguale a x:
b y = x
Allora il logaritmo in base b di x è uguale a y:
log b ( x ) = y
Ad esempio quando:
2 4 = 16
Poi
log 2 (16) = 4
Logaritmo come funzione inversa della funzione esponenziale
La funzione logaritmica,
y = log b ( x )
è la funzione inversa della funzione esponenziale,
x = b y
Quindi se calcoliamo la funzione esponenziale del logaritmo di x (x/ 0),
f ( f -1 ( x )) = b log b ( x ) = x
Oppure se calcoliamo il logaritmo della funzione esponenziale di x,
f -1 ( f ( x )) = log b ( b x ) = x
Logaritmo naturale (ln)
Il logaritmo naturale è un logaritmo in base e:
ln ( x ) = log e ( x )
Quando la costante è il numero:
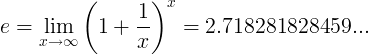
o
![]()
Vedi: logaritmo naturale
Calcolo del logaritmo inverso
Il logaritmo inverso (o anti logaritmo) viene calcolato elevando la base b al logaritmo y:
x = log -1 ( y ) = b y
Funzione logaritmica
La funzione logaritmica ha la forma base di:
f ( x ) = log b ( x )
Regole logaritmiche
| Nome regola | Regola |
|---|---|
Regola del prodotto logaritmo |
log b ( x ∙ y ) = log b ( x ) + log b ( y ) |
Regola del quoziente logaritmico |
log b ( x / y ) = log b ( x ) - log b ( y ) |
Regola del potere logaritmico |
log b ( x y ) = y ∙ log b ( x ) |
Regola di commutazione di base del logaritmo |
log b ( c ) = 1 / log c ( b ) |
Regola di modifica della base del logaritmo |
log b ( x ) = log c ( x ) / log c ( b ) |
Derivata del logaritmo |
f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b )) |
Integrale del logaritmo |
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C |
Logaritmo del numero negativo |
log b ( x ) non è definito quando x ≤ 0 |
Logaritmo di 0 |
log b (0) non è definito |
Logaritmo di 1 |
log b (1) = 0 |
Logaritmo della base |
log b ( b ) = 1 |
Logaritmo dell'infinito |
lim log b ( x ) = ∞, quando x → ∞ |
Vedi: regole del logaritmo
Regola del prodotto logaritmo
Il logaritmo della moltiplicazione di xey è la somma del logaritmo di xe del logaritmo di y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Per esempio:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Regola del quoziente logaritmico
Il logaritmo della divisione di x e y è la differenza tra il logaritmo di x e il logaritmo di y.
log b ( x / y ) = log b ( x ) - log b ( y )
Per esempio:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Regola del potere logaritmico
Il logaritmo di x elevato alla potenza di y è y volte il logaritmo di x.
log b ( x y ) = y ∙ log b ( x )
Per esempio:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Regola di commutazione di base del logaritmo
Il logaritmo in base b di c è 1 diviso per il logaritmo in base c di b.
log b ( c ) = 1 / log c ( b )
Per esempio:
log 2 (8) = 1 / log 8 (2)
Regola di modifica della base del logaritmo
Il logaritmo in base b di x è il logaritmo in base c di x diviso per il logaritmo in base c di b.
log b ( x ) = log c ( x ) / log c ( b )
Ad esempio, per calcolare il log 2 (8) nella calcolatrice, dobbiamo cambiare la base in 10:
log 2 (8) = log 10 (8) / log 10 (2)
Vedere: regola di modifica della base del registro
Logaritmo del numero negativo
Il logaritmo reale in base b di x quando x <= 0 non è definito quando x è negativo o uguale a zero:
log b ( x ) non è definito quando x ≤ 0
Vedi: log del numero negativo
Logaritmo di 0
Il logaritmo in base b di zero non è definito:
log b (0) non è definito
Il limite del logaritmo in base b di x, quando x si avvicina a zero, è meno infinito:
![]()
Vedi: log di zero
Logaritmo di 1
Il logaritmo in base b di uno è zero:
log b (1) = 0
Ad esempio, il logaritmo in base due di uno è zero:
log 2 (1) = 0
Vedi: log di uno
Logaritmo dell'infinito
Il limite del logaritmo in base b di x, quando x tende a infinito, è uguale a infinito:
lim log b ( x ) = ∞, quando x → ∞
Vedi: log dell'infinito
Logaritmo della base
Il logaritmo in base b di b è uno:
log b ( b ) = 1
Ad esempio, il logaritmo in base due di due è uno:
log 2 (2) = 1
Derivata del logaritmo
quando
f ( x ) = log b ( x )
Quindi la derivata di f (x):
f ' ( x ) = 1 / ( x ln ( b ))
Vedi: derivata logaritmica
Integrale logaritmo
L'integrale del logaritmo di x:
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
Per esempio:
∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) - 1 / ln (2) ) + C
Approssimazione logaritmica
log 2 ( x ) ≈ n + ( x / 2 n - 1),
Logaritmo complesso
Per il numero complesso z:
z = re iθ = x + iy
Il logaritmo complesso sarà (n = ...- 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
Problemi e risposte di logaritmo
Problema n. 1
Trova x per
log 2 ( x ) + log 2 ( x -3) = 2
Soluzione:
Utilizzando la regola del prodotto:
log 2 ( x ∙ ( x -3)) = 2
Modifica della forma del logaritmo in base alla definizione del logaritmo:
x ∙ ( x -3) = 2 2
Oppure
x 2 -3 x -4 = 0
Risolvere l'equazione quadratica:
x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1
Poiché il logaritmo non è definito per i numeri negativi, la risposta è:
x = 4
Problema n. 2
Trova x per
log 3 ( x +2) - log 3 ( x ) = 2
Soluzione:
Utilizzando la regola del quoziente:
log 3 (( x +2) / x ) = 2
Modifica della forma del logaritmo in base alla definizione del logaritmo:
( x +2) / x = 3 2
Oppure
x +2 = 9 x
Oppure
8 x = 2
Oppure
x = 0,25
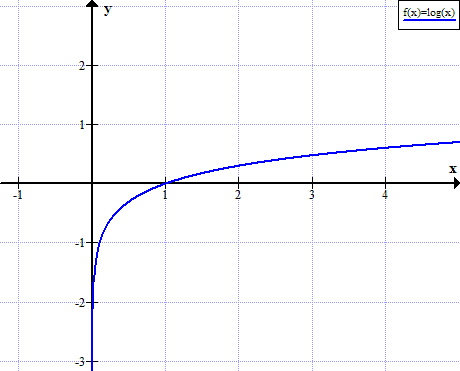
Grafico del log (x)
log (x) non è definito per valori reali non positivi di x:
Tabella dei logaritmi
| x | log 10 x | log 2 x | log e x |
|---|---|---|---|
| 0 | non definito | non definito | non definito |
| 0 + | - ∞ | - ∞ | - ∞ |
| 0.0001 | -4 | -13.287712 | -9.210340 |
| 0.001 | -3 | -9.965784 | -6.907755 |
| 0,01 | -2 | -6.643856 | -4.605170 |
| 0.1 | -1 | -3.321928 | -2.302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0.301030 | 1 | 0.693147 |
| 3 | 0.477121 | 1.584963 | 1.098612 |
| 4 | 0.602060 | 2 | 1.386294 |
| 5 | 0.698970 | 2.321928 | 1.609438 |
| 6 | 0.778151 | 2.584963 | 1.791759 |
| 7 | 0.845098 | 2.807355 | 1.945910 |
| 8 | 0.903090 | 3 | 2.079442 |
| 9 | 0.954243 | 3.169925 | 2.197225 |
| 10 | 1 | 3.321928 | 2.302585 |
| 20 | 1.301030 | 4.321928 | 2.995732 |
| 30 | 1.477121 | 4.906891 | 3.401197 |
| 40 | 1.602060 | 5.321928 | 3.688879 |
| 50 | 1.698970 | 5.643856 | 3.912023 |
| 60 | 1.778151 | 5.906991 | 4.094345 |
| 70 | 1.845098 | 6.129283 | 4.248495 |
| 80 | 1.903090 | 6.321928 | 4.382027 |
| 90 | 1.954243 | 6.491853 | 4.499810 |
| 100 | 2 | 6.643856 | 4.605170 |
| 200 | 2.301030 | 7.643856 | 5.298317 |
| 300 | 2.477121 | 8.228819 | 5.703782 |
| 400 | 2.602060 | 8.643856 | 5.991465 |
| 500 | 2.698970 | 8.965784 | 6.214608 |
| 600 | 2.778151 | 9.228819 | 6.396930 |
| 700 | 2.845098 | 9.451211 | 6.551080 |
| 800 | 2.903090 | 9.643856 | 6.684612 |
| 900 | 2.954243 | 9.813781 | 6.802395 |
| 1000 | 3 | 9.965784 | 6.907755 |
| 10000 | 4 | 13.287712 | 9.210340 |
Guarda anche
- Regole logaritmiche
- Cambio logaritmo di base
- Logaritmo di zero
- Logaritmo di uno
- Logaritmo dell'infinito
- Logaritmo del numero negativo
- Calcolatrice logaritmo
- Grafico logaritmo
- Tabella dei logaritmi
- Calcolatore del logaritmo naturale
- Logaritmo naturale - ln x
- e costante
- Decibel (dB)