e costante
La costante o il numero di Eulero è una costante matematica. La costante e è un numero reale e irrazionale.
e = 2,718281828459 ...
Definizione di e
La costante e è definita come limite:
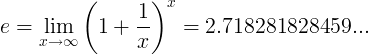
Definizioni alternative
La costante e è definita come limite:
![]()
La costante e è definita come la serie infinita:
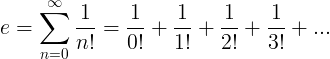
Proprietà di e
Reciproco di e
Il reciproco di e è il limite:
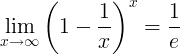
Derivati di e
La derivata della funzione esponenziale è la funzione esponenziale:
( e x ) '= e x
La derivata della funzione logaritmo naturale è la funzione reciproca:
(log e x ) '= (ln x )' = 1 / x
Integrali di e
L'integrale indefinito della funzione esponenziale e x è la funzione esponenziale e x .
∫ e x dx = e x + c
L'integrale indefinito della funzione logaritmo naturale log e x è:
∫ log e x dx = ∫ ln x dx = x ln x - x + c
L'integrale definito da 1 a e della funzione reciproca 1 / x è 1:
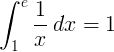
Base e logaritmo
Il logaritmo naturale di un numero x è definito come il logaritmo in base e di x:
ln x = log e x
Funzione esponenziale
La funzione esponenziale è definita come:
f ( x ) = exp ( x ) = e x
Formula di Eulero
Il numero complesso e iθ ha l'identità:
e ioθ = cos ( θ ) + i sin ( θ )
i è l'unità immaginaria (la radice quadrata di -1).
θ è un numero reale.
Guarda anche
- Come e è 2.71828183?
- Regole logaritmiche
- Logaritmo naturale
- Regole degli esponenti
- Distribuzione normale
- Pi costante
- e costante - wikipedia