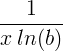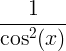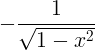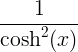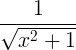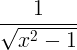파생 규칙

파생 규칙 및 법률. 함수 테이블의 파생물.

함수의 미분은 Δx가 무한히 작을 때 Δx가있는 지점 x + Δx 및 x에서 함수 값 f (x)의 차이의 비율입니다. 미분은 점 x에서 접선의 함수 기울기 또는 기울기입니다.

$f '(x) = \ lim _ {\ Delta x \ to 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}$

2 차 도함수는 다음과 같이 지정됩니다.

또는 단순히 1 차 도함수를 유도하십시오.

N 번째 유도체 F (x)를 n 회를 도출함으로써 계산된다.

N 번째 유도체는 N-1 유도체의 유도체 동일 :

f ^{( n )} ( x ) = [ f ^{( n -1)} ( x )] '

4 차 도함수 찾기

f ( x ) = 2 x ⁵

f ⁽⁴⁾ ( x ) = [2 x ⁵ ] '' ''= [10 x ⁴ ] '' '= [40 x ³ ]' '= [120 x ² ]'= 240 x

함수의 미분은 접선의 기울기입니다.

미분 합계 규칙	( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
파생 상품 규칙	( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
미분 몫 규칙	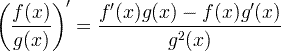$\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f'(x) g (x) -f (x) g '(x)} {g ^ 2 ( 엑스)}$
파생 체인 규칙	f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

a 와 b 가 상수 일 때 .

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

도함수 찾기 :

3 x ² + 4 x.

합계 규칙에 따르면 :

a = 3, b = 4

f ( x ) = x ² , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x ² + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

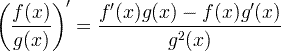
$\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f'(x) g (x) -f (x) g '(x)} {g ^ 2 ( 엑스)}$

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

이 규칙은 Lagrange의 표기법으로 더 잘 이해할 수 있습니다.

$\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}$

작은 Δx의 경우 f (x ₀ ) 및 f '(x ₀ )을 알고있을 때 f (x ₀ + Δx)에 대한 근사치를 얻을 수 있습니다 .

f ( x ₀ + Δ x ) ≈ f ( x ₀ ) + f '( x ₀ ) ⋅Δ x