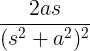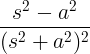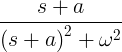라플라스 변환

라플라스 변환은 0에서 무한대로 통합하여 시간 도메인 함수를 s 도메인 함수로 변환합니다.

시간 도메인 함수에 e ^-st를 곱합니다 .

Laplace 변환은 미분 방정식과 적분에 대한 해를 빠르게 찾는 데 사용됩니다.

시간 영역의 유도는 s 영역에서 s의 곱셈으로 변환됩니다.

시간 영역의 적분은 s 영역의 s로 나누기로 변환됩니다.

라플라스 변환 함수

Laplace 변환은 L {} 연산자로 정의됩니다 .

$F (s) = \ mathcal {L} \ left \ {f (t) \ right \} = \ int_ {0} ^ {\ infty} e ^ {-st} f (t) dt$

역 라플라스 변환은 직접 계산할 수 있습니다.

일반적으로 역변환은 변환 테이블에서 제공됩니다.

기능 명	시간 영역 기능	라플라스 변환
기능 명	에프 ( t )	F ( 초 ) = L { f ( t )}
일정한	1	$\ frac {1} {s}$
선의	t	$\ frac {1} {s ^ 2}$
힘	t ⁿ	$\ frac {n!} {s ^ {n + 1}}$
힘	t ^a	Γ ( a +1) ⋅ s- ^{( a +1)}
멱지수	e ^at	$\ frac {1} {sa}$
사인	죄 를 짓다	$\ frac {a} {s ^ 2 + a ^ 2}$
코사인	COS 에서	$\ frac {s} {s ^ 2 + a ^ 2}$
쌍곡 사인	SINH 에서	$\ frac {a} {s ^ 2-a ^ 2}$
쌍곡 코사인	곤봉 에서	$\ frac {s} {s ^ 2-a ^ 2}$
증가하는 사인	t의 죄 에서	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
코사인 증가	t cos at	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
썩어가는 사인	전자 ^-at 죄 고주파 영역	$\ frac {\ omega} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
쇠퇴하는 코사인	e ^-at cos ωt	$\ frac {s + a} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
델타 기능	δ ( t )	1
지연된 델타	δ ( ta )	e ^-as

부동산 이름	시간 영역 기능	라플라스 변환	논평
	에프 ( t )	F ( 초 )
선형성	af ( t ) + bg ( t )	aF ( s ) + bG ( s )	a , b 는 일정합니다.
규모 변경	f ( 에서 )	$\ frac {1} {a} F \ left (\ frac {s} {a} \ right)$	a / 0
시프트	e ^-at f ( t )	F ( s + a )
지연	f ( 타 )	전자 ^{- 같은} F ( S )
유도	$\ frac {df (t)} {dt}$	sF ( s ) -f (0)
N 번째 유도	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) -s ^{n -1}f (0) -s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
힘	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
완성	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F (s)$
역수	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
회선	f ( t ) * g ( t )	F ( 초 ) ⋅ G ( 초 )	*는 컨볼 루션 연산자입니다.
주기적 기능	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {-sT}} \ int_ {0} ^ {T} e ^ {-sx} f (x) dx$