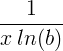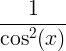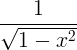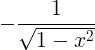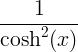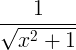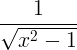Peraturan terbitan
Peraturan dan undang-undang derivatif. Jadual derivatif fungsi.
Definisi terbitan
Derivatif suatu fungsi adalah nisbah perbezaan nilai fungsi f (x) pada titik x + Δx dan x dengan Δx, ketika Δx kecil secara kecil. Derivatifnya adalah cerun fungsi atau cerun garis tangen pada titik x.
![]()
Derivatif kedua
Derivatif kedua diberikan oleh:
![]()
Atau dapatkan derivatif pertama:
![]()
Derivatif ke-9
The n terbitan th dikira dengan memperolehi f (x) n masa.
The n th derivatif adalah sama dengan terbitan (n-1) terbitan:
f ( n ) ( x ) = [ f ( n -1) ( x )] '
Contoh:
Cari terbitan keempat dari
f ( x ) = 2 x 5
f (4) ( x ) = [2 x 5 ] "" = [10 x 4 ] "" = [40 x 3 ] "= [120 x 2 ]" = 240 x
Derivatif pada graf fungsi
Derivatif suatu fungsi adalah kemerosotan garis tangen.
Peraturan terbitan
| Peraturan jumlah terbitan | ( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x ) |
| Peraturan produk terbitan | ( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x ) |
| Peraturan hasil terbitan | 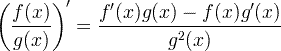 |
| Peraturan rantai derivatif | f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x ) |
Peraturan jumlah terbitan
Apabila a dan b adalah pemalar.
( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Contoh:
Cari terbitan dari:
3 x 2 + 4 x.
Menurut peraturan jumlah:
a = 3, b = 4
f ( x ) = x 2 , g ( x ) = x
f ' ( x ) = 2 x , g' ( x ) = 1
(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4
Peraturan produk terbitan
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Peraturan hasil terbitan
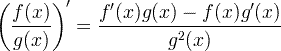
Peraturan rantai derivatif
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )
Peraturan ini dapat difahami dengan lebih baik dengan notasi Lagrange:
![]()
Fungsi penghampiran linear
Untuk Δx kecil, kita dapat memperoleh perkiraan untuk f (x 0 + Δx), ketika kita mengetahui f (x 0 ) dan f '(x 0 ):
f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x
Jadual derivatif fungsi
| Nama fungsi | Fungsi | Derivatif |
|---|---|---|
| f ( x ) |
f '( x ) | |
| Pemalar | penyambung |
0 |
| Linier | x |
1 |
| Kuasa | x a |
kapak a- 1 |
| Eksponensial | e x |
e x |
| Eksponensial | sebuah x |
a x ln a |
| Logaritma semula jadi | ln ( x ) |
|
| Logaritma | log b ( x ) |
|
| Benar | dosa x |
cos x |
| Kosinus | cos x |
-sin x |
| Tangen | tan x |
|
| Arcsine | arcsin x |
|
| Arccosine | arccos x |
|
| Arctangent | arctan x |
|
| Sinus hiperbolik | sinh x |
cos x |
| Kosinus hiperbolik | cos x |
sinh x |
| Tangen hiperbolik | tanh x |
|
| Sinus hiperbolik terbalik | sinh -1 x |
|
| Kosinus hiperbolik terbalik | cosh -1 x |
|
| Tangen hiperbolik terbalik | tanh -1 x |
|
Contoh terbitan
Contoh # 1
f ( x ) = x 3 +5 x 2 + x +8
f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1
Contoh # 2
f ( x ) = sin (3 x 2 )
Semasa menggunakan peraturan rantai:
f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x
Ujian terbitan kedua
Apabila terbitan pertama fungsi adalah sifar pada titik x 0 .
f '( x 0 ) = 0
Maka terbitan kedua pada titik x 0 , f '' (x 0 ), dapat menunjukkan jenis titik itu:
| f '' ( x 0 )/ 0 |
minimum tempatan |
| f '' ( x 0 ) <0 |
maksimum tempatan |
| f '' ( x 0 ) = 0 |
tidak dapat ditentukan |