Równanie kwadratowe
Równanie kwadratowe jest wielomianem drugiego rzędu o 3 współczynnikach - a , b , c .
Równanie kwadratowe jest określone wzorem:
ax 2 + bx + c = 0
Rozwiązanie równania kwadratowego daje 2 liczby x 1 i x 2 .
Możemy zmienić równanie kwadratowe do postaci:
( x - x 1 ) ( x - x 2 ) = 0
Równanie kwadratowe
Rozwiązanie równania kwadratowego podaje wzór kwadratowy:
![]()
Wyrażenie wewnątrz pierwiastka kwadratowego nazywa się dyskryminacją i jest oznaczone przez Δ:
Δ = b 2 - 4 AC
Wzór kwadratowy z notacją dyskryminacyjną:
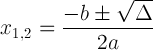
To wyrażenie jest ważne, ponieważ może nam powiedzieć o rozwiązaniu:
- Gdy Δ/ 0, istnieją 2 pierwiastki rzeczywiste x 1 = (- b + √ Δ ) / (2a) i x 2 = (- b-√ Δ ) / (2a) .
- Gdy Δ = 0, istnieje jeden pierwiastek x 1 = x 2 = -b / (2a) .
- Gdy Δ <0, nie istnieją żadne realne korzenie, są złożone korzenie: 2
x 1 = (- b + i√ -Δ ) / (2a), a x 2 = (- bi√ -Δ ) / (2a) .
Problem nr 1
3 x 2 +5 x +2 = 0
rozwiązanie:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Problem nr 2
3 x 2 -6 x + 3 = 0
rozwiązanie:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Problem nr 3
x 2 +2 x +5 = 0
rozwiązanie:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Nie ma prawdziwych rozwiązań. Wartości są liczbami zespolonymi:
x 1 = -1 + 2 i
x 2 = 1 - 2 i
Kwadratowy wykres funkcji
Funkcja kwadratowa jest funkcją wielomianu drugiego rzędu:
f ( x ) = ax 2 + bx + c
Rozwiązaniem równania kwadratowego są pierwiastki funkcji kwadratowej, czyli punkty przecięcia wykresu funkcji kwadratowej z osią x, gdy
f ( x ) = 0
Gdy istnieją 2 punkty przecięcia wykresu z osią x, istnieją 2 rozwiązania równania kwadratowego.
Gdy istnieje 1 punkt przecięcia wykresu z osią x, istnieje 1 rozwiązanie równania kwadratowego.
Gdy nie ma punktów przecięcia wykresu z osią X, nie otrzymujemy rzeczywistych rozwiązań (lub 2 złożone rozwiązania).