Reguły logarytmu
Podstawa b logarytm z liczby to wykładnik że musimy podnieść podstawę w celu uzyskania numeru.
- Definicja logarytmu
- Reguły logarytmu
- Problemy logarytmiczne
- Złożony logarytm
- Wykres log (x)
- Tablica logarytmów
- Kalkulator logarytmów
Definicja logarytmu
Kiedy b jest podniesione do potęgi y jest równe x:
b y = x
Wtedy logarytm o podstawie b z x jest równy y:
log b ( x ) = y
Na przykład gdy:
2 4 = 16
Następnie
log 2 (16) = 4
Logarytm jako funkcja odwrotna funkcji wykładniczej
Funkcja logarytmiczna,
y = log b ( x )
jest funkcją odwrotną funkcji wykładniczej,
x = b y
Jeśli więc obliczymy wykładniczą funkcję logarytmu x (x/ 0),
f ( f -1 ( x )) = b log b ( x ) = x
Lub jeśli obliczymy logarytm funkcji wykładniczej x,
f -1 ( f ( x )) = log b ( b x ) = x
Logarytm naturalny (ln)
Logarytm naturalny to logarytm o podstawie e:
ln ( x ) = log e ( x )
Gdy e stała jest liczbą:
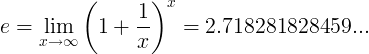
lub
![]()
Zobacz: logarytm naturalny
Obliczanie odwrotnego logarytmu
Odwrotny logarytm (lub antylogarytm) oblicza się, podnosząc podstawę b do logarytmu y:
x = log -1 ( y ) = b y
Funkcja logarytmiczna
Funkcja logarytmiczna ma podstawową postać:
f ( x ) = log b ( x )
Reguły logarytmu
| Nazwa reguły | Reguła |
|---|---|
Reguła iloczynu logarytmicznego |
log b ( x ∙ y ) = log b ( x ) + log b ( y ) |
Reguła ilorazu logarytmu |
log b ( x / y ) = log b ( x ) - log b ( y ) |
Reguła potęgi logarytmów |
log b ( x y ) = y ∙ log b ( x ) |
Reguła przełączania podstawy logarytmu |
log b ( c ) = 1 / log c ( b ) |
Reguła zmiany podstawy logarytmu |
log b ( x ) = log c ( x ) / log c ( b ) |
Pochodna logarytmu |
f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b )) |
Całka logarytmu |
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C |
Logarytm liczby ujemnej |
log b ( x ) jest niezdefiniowane, gdy x ≤ 0 |
Logarytm 0 |
log b (0) jest niezdefiniowane |
Logarytm 1 |
log b (1) = 0 |
Logarytm podstawy |
log b ( b ) = 1 |
Logarytm nieskończoności |
lim log b ( x ) = ∞, gdy x → ∞ |
Zobacz: Reguły logarytmu
Reguła iloczynu logarytmicznego
Logarytm mnożenia x i y jest sumą logarytmu x i logarytmu y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Na przykład:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Reguła ilorazu logarytmu
Logarytm z dzielenia xiy jest różnicą logarytmu z x i logarytmu z y.
log b ( x / y ) = log b ( x ) - log b ( y )
Na przykład:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Reguła potęgi logarytmów
Logarytm x podniesiony do potęgi y to y razy logarytm z x.
log b ( x y ) = y ∙ log b ( x )
Na przykład:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Reguła przełączania podstawy logarytmu
Logarytm o podstawie b z c wynosi 1 podzielony przez logarytm o podstawie c z b.
log b ( c ) = 1 / log c ( b )
Na przykład:
log 2 (8) = 1 / log 8 (2)
Reguła zmiany podstawy logarytmu
Logarytm o podstawie b z x to logarytm o podstawie c z x podzielony przez logarytm o podstawie c z liczby b.
log b ( x ) = log c ( x ) / log c ( b )
Na przykład, aby obliczyć log 2 (8) w kalkulatorze, musimy zmienić podstawę na 10:
log 2 (8) = log 10 (8) / log 10 (2)
Zobacz: reguła zmiany podstawy dziennika
Logarytm liczby ujemnej
Logarytm rzeczywisty o podstawie b x, gdy x <= 0 jest niezdefiniowany, gdy x jest ujemne lub równe zero:
log b ( x ) jest niezdefiniowane, gdy x ≤ 0
Zobacz: log liczby ujemnej
Logarytm 0
Podstawowy logarytm b zero jest niezdefiniowany:
log b (0) jest niezdefiniowane
Granica logarytmu podstawy b z x, gdy x zbliża się do zera, jest minus nieskończoność:
![]()
Zobacz: log of zero
Logarytm 1
Podstawowy logarytm b z jedynki wynosi zero:
log b (1) = 0
Na przykład logarytm o podstawie dwóch z jednego jest równy zero:
log 2 (1) = 0
Zobacz: log z jednego
Logarytm nieskończoności
Granica logarytmu podstawy b z x, gdy x zbliża się do nieskończoności, jest równa nieskończoności:
lim log b ( x ) = ∞, gdy x → ∞
Zobacz: log nieskończoności
Logarytm podstawy
Podstawowy logarytm b z b to jeden:
log b ( b ) = 1
Na przykład logarytm o podstawie dwa z dwóch to jeden:
log 2 (2) = 1
Pochodna logarytmu
Gdy
f ( x ) = log b ( x )
Następnie pochodna f (x):
f ' ( x ) = 1 / ( x ln ( b ))
Zobacz: pochodna logarytmiczna
Całka logarytmiczna
Całka z logarytmu x:
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
Na przykład:
∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) - 1 / ln (2) ) + C
Przybliżenie logarytmu
log 2 ( x ) ≈ n + ( x / 2 n - 1),
Złożony logarytm
Dla liczby zespolonej z:
z = re iθ = x + iy
Złożony logarytm wyniesie (n = ...- 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
Problemy i odpowiedzi logarytmiczne
Problem nr 1
Znajdź x dla
log 2 ( x ) + log 2 ( x -3) = 2
Rozwiązanie:
Korzystanie z reguły iloczynu:
log 2 ( x ∙ ( x -3)) = 2
Zmiana postaci logarytmu zgodnie z definicją logarytmu:
x ∙ ( x -3) = 2 2
Lub
x 2 -3 x -4 = 0
Rozwiązanie równania kwadratowego:
x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1
Ponieważ logarytm nie jest zdefiniowany dla liczb ujemnych, odpowiedź brzmi:
x = 4
Problem nr 2
Znajdź x dla
log 3 ( x +2) - log 3 ( x ) = 2
Rozwiązanie:
Stosując regułę ilorazu:
log 3 (( x +2) / x ) = 2
Zmiana postaci logarytmu zgodnie z definicją logarytmu:
( x +2) / x = 3 2
Lub
x +2 = 9 x
Lub
8 x = 2
Lub
x = 0,25
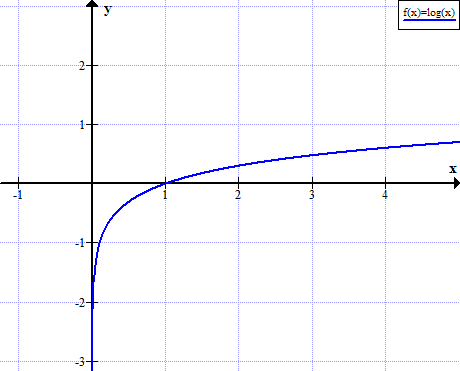
Wykres log (x)
log (x) nie jest zdefiniowany dla rzeczywistych niedodatnich wartości x:
Tablica logarytmów
| x | logować 10 x | log 2 x | log e x |
|---|---|---|---|
| 0 | nieokreślony | nieokreślony | nieokreślony |
| 0 + | - ∞ | - ∞ | - ∞ |
| 0,0001 | -4 | -13,287712 | -9,210340 |
| 0,001 | -3 | -9,965784 | -6.907755 |
| 0,01 | -2 | -6,643856 | -4,605170 |
| 0.1 | -1 | -3,321928 | -2,302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0,301030 | 1 | 0.693147 |
| 3 | 0,477121 | 1.584963 | 1.098612 |
| 4 | 0,602060 | 2 | 1.386294 |
| 5 | 0.698970 | 2.321928 | 1.609438 |
| 6 | 0,778151 | 2.584963 | 1.791759 |
| 7 | 0.845098 | 2.807355 | 1.945910 |
| 8 | 0,903090 | 3 | 2.079442 |
| 9 | 0.954243 | 3.169925 | 2.197225 |
| 10 | 1 | 3.321928 | 2.302585 |
| 20 | 1.301030 | 4.321928 | 2.995732 |
| 30 | 1.477121 | 4.906891 | 3.401197 |
| 40 | 1.602060 | 5.321928 | 3.688879 |
| 50 | 1.698970 | 5.643856 | 3,912023 |
| 60 | 1.778151 | 5.906991 | 4.094345 |
| 70 | 1.845098 | 6.129283 | 4.248495 |
| 80 | 1.903090 | 6.321928 | 4.382027 |
| 90 | 1.954243 | 6.491853 | 4.499810 |
| 100 | 2 | 6.643856 | 4.605170 |
| 200 | 2.301030 | 7,643856 | 5.298317 |
| 300 | 2.477121 | 8.228819 | 5.703782 |
| 400 | 2.602060 | 8.643856 | 5,991465 |
| 500 | 2.698970 | 8,965784 | 6.214608 |
| 600 | 2,778151 | 9.228819 | 6.396930 |
| 700 | 2.845098 | 9.451211 | 6.551080 |
| 800 | 2.903090 | 9,643856 | 6.684612 |
| 900 | 2,954243 | 9.813781 | 6.802395 |
| 1000 | 3 | 9,965784 | 6.907755 |
| dziesięć tysięcy | 4 | 13.287712 | 9.210340 |
Zobacz też
- Reguły logarytmu
- Zmiana logarytmu podstawy
- Logarytm zera
- Logarytm jednego
- Logarytm nieskończoności
- Logarytm liczby ujemnej
- Kalkulator logarytmów
- Wykres logarytmiczny
- Tablica logarytmów
- Kalkulator logarytmu naturalnego
- Logarytm naturalny - ln x
- e stała
- Decybel (dB)