కన్వల్యూషన్
రివర్స్డ్ ఫంక్షన్ g (t-τ) తో f (τ) యొక్క పరస్పర సంబంధం ఫంక్షన్.
కన్వల్యూషన్ ఆపరేటర్ ఆస్టరిస్క్ చిహ్నం * .
- నిరంతర కన్వల్యూషన్
- వివిక్త కన్వల్యూషన్
- 2 డి వివిక్త కన్వల్యూషన్
- కన్విలేషన్తో ఫిల్టర్ అమలు
- కన్వల్యూషన్ సిద్ధాంతం
నిరంతర కన్వల్యూషన్
F (t) మరియు g (t) యొక్క కన్వల్యూషన్ f (τ) సార్లు f (t-τ) యొక్క సమగ్రానికి సమానం:
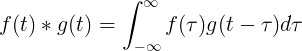
వివిక్త కన్వల్యూషన్
2 వివిక్త ఫంక్షన్ల యొక్క కన్వల్యూషన్ ఇలా నిర్వచించబడింది:
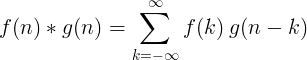
2 డి వివిక్త కన్వల్యూషన్
ఇమేజ్ ప్రాసెసింగ్ కోసం 2 డైమెన్షనల్ వివిక్త కన్వల్యూషన్ సాధారణంగా ఉపయోగించబడుతుంది.
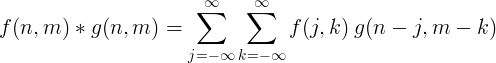
కన్విలేషన్తో ఫిల్టర్ అమలు
అవుట్పుట్ సిగ్నల్ y (n) ను పొందడానికి ప్రేరణ స్పందన h (n) తో కన్విలేషన్ ద్వారా వివిక్త ఇన్పుట్ సిగ్నల్ x (n) ను ఫిల్టర్ చేయవచ్చు.
y ( n ) = x ( n ) * h ( n )
కన్వల్యూషన్ సిద్ధాంతం
2 ఫంక్షన్ల గుణకారం యొక్క ఫోరియర్ పరివర్తన ప్రతి ఫంక్షన్ యొక్క ఫోరియర్ పరివర్తనాల యొక్క కన్వల్యూషన్కు సమానం:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
2 ఫంక్షన్ల యొక్క కన్విలేషన్ యొక్క ఫోరియర్ పరివర్తన ప్రతి ఫంక్షన్ యొక్క ఫోరియర్ పరివర్తనాల గుణకారానికి సమానం:
ℱ { f * g } = ℱ { f } ⋅ g { g }
నిరంతర ఫోరియర్ పరివర్తన కోసం కన్వల్యూషన్ సిద్ధాంతం
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
వివిక్త ఫోరియర్ పరివర్తన కోసం కన్వల్యూషన్ సిద్ధాంతం
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
లాప్లేస్ పరివర్తన కోసం కన్వల్యూషన్ సిద్ధాంతం
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( లు ) ⋅ G ( లు )
ఇది కూడ చూడు
కాలిక్యులస్
- పరిమితి
- ఉత్పన్నం
- సమగ్ర
- సిరీస్
- లాప్లేస్ పరివర్తన
- కన్వల్యూషన్
- కాలిక్యులస్ చిహ్నాలు
రాపిడ్ టేబుల్స్