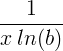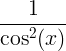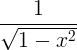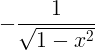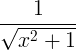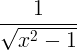ఉత్పన్న నియమాలు

ఉత్పన్న నియమాలు మరియు చట్టాలు. ఫంక్షన్ల పట్టిక యొక్క ఉత్పన్నాలు.

ఉత్పన్న నిర్వచనం

ఫంక్షన్ యొక్క ఉత్పన్నం x (x) పాయింట్ల వద్ద ఫంక్షన్ విలువ f (x) మరియు x withx తో x యొక్క వ్యత్యాసం యొక్క నిష్పత్తి, Δx అనంతంగా చిన్నగా ఉన్నప్పుడు. పాయింట్ x వద్ద టాంజెంట్ లైన్ యొక్క ఫంక్షన్ వాలు లేదా వాలు ఉత్పన్నం.

 

f '(x) = \ lim _ {\ డెల్టా x \ నుండి 0} \ frac {f (x + \ డెల్టా x) -f (x)} {\ డెల్టా x}

రెండవ ఉత్పన్నం

రెండవ ఉత్పన్నం వీరిచే ఇవ్వబడింది:

లేదా మొదటి ఉత్పన్నం ఉత్పన్నం:

f '' (x) = (f '(x))'

N వ ఉత్పన్నం

N వ ఉత్పన్నం f (x) n సార్లు తీసుకోబడిన లెక్కించబడుతుంది.

N వ ఉత్పన్నం (n-1) ఉత్పన్న ఉత్పన్న సమం:

f ( n ) ( x ) = [ f ( n -1) ( x )] '

ఉదాహరణ:

యొక్క నాల్గవ ఉత్పన్నం కనుగొనండి

f ( x ) = 2 x 5

f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '[[40 x 3 ]' '= [120 x 2 ]' = 240 x

ఫంక్షన్ గ్రాఫ్ పై ఉత్పన్నం

ఒక ఫంక్షన్ యొక్క ఉత్పన్నం టాంజెన్షియల్ లైన్ యొక్క వాలు.

ఉత్పన్న నియమాలు

ఉత్పన్న మొత్తం నియమం

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
ఉత్పన్న ఉత్పత్తి నియమం

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
ఉత్పన్న కోటీన్ నియమం 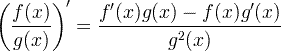\ ఎడమ (\ frac {f (x)} {g (x)} \ కుడి) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}
ఉత్పన్న గొలుసు నియమం

f ( g ( x )) '= f' ( g ( x )) g ' ( x )

ఉత్పన్న మొత్తం నియమం

చేసినప్పుడు ఒక మరియు బి స్థిరాంకాలు ఉంటాయి.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

ఉదాహరణ:

దీని ఉత్పన్నం కనుగొనండి:

3 x 2 + 4 x.

మొత్తం నియమం ప్రకారం:

a = 3, బి = 4

f ( x ) = x 2 , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

ఉత్పన్న ఉత్పత్తి నియమం

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

ఉత్పన్న కోటీన్ నియమం

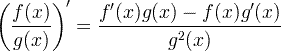
\ ఎడమ (\ frac {f (x)} {g (x)} \ కుడి) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}

ఉత్పన్న గొలుసు నియమం

f ( g ( x )) '= f' ( g ( x )) g ' ( x )

లాగ్రేంజ్ యొక్క సంజ్ఞామానంతో ఈ నియమాన్ని బాగా అర్థం చేసుకోవచ్చు:

\ frac {df} {dx} = \ frac {df} {dg} d cdot \ frac {dg} x dx}

ఫంక్షన్ సరళ ఉజ్జాయింపు

చిన్న Δx కొరకు, మనకు f (x 0 + Δx) కు ఒక ఉజ్జాయింపు పొందవచ్చు , మనకు f (x 0 ) మరియు f '(x 0 ) తెలిసినప్పుడు :

f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) x

ఫంక్షన్ల పట్టిక యొక్క ఉత్పన్నాలు

ఫంక్షన్ పేరు ఫంక్షన్ ఉత్పన్నం

f ( x )

 f '( x )
స్థిరంగా

const

0

లీనియర్

x

1

శక్తి

x a

గొడ్డలి a- 1
ఘాతాంకం

e x

e x
ఘాతాంకం

a x

a x ln a
సహజ లాగరిథం

ln ( x )

లోగరిథం

లాగ్ బి ( x )

సైన్

పాపం x

cos x
కొసైన్

cos x

-సిన్ x
టాంజెంట్

తాన్ x

ఆర్క్సిన్

ఆర్క్సిన్ x

ఆర్కోసిన్

ఆర్కోస్ x

ఆర్క్టాంజెంట్

ఆర్క్టాన్ x
హైపర్బోలిక్ సైన్

sinh x

cosh x
హైపర్బోలిక్ కొసైన్

cosh x

sinh x
హైపర్బోలిక్ టాంజెంట్

tanh x

విలోమ హైపర్బోలిక్ సైన్

sinh -1 x

విలోమ హైపర్బోలిక్ కొసైన్

cosh -1 x

విలోమ హైపర్బోలిక్ టాంజెంట్

tanh -1 x

ఉత్పన్న ఉదాహరణలు

ఉదాహరణ # 1

f ( x ) = x 3 +5 x 2 + x +8

f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1

ఉదాహరణ # 2

f ( x ) = పాపం (3 x 2 )

గొలుసు నియమాన్ని వర్తించేటప్పుడు:

f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x

రెండవ ఉత్పన్న పరీక్ష

ఫంక్షన్ యొక్క మొదటి ఉత్పన్నం పాయింట్ x 0 వద్ద సున్నా అయినప్పుడు .

f '( x 0 ) = 0

అప్పుడు పాయింట్ x 0 , f '' (x 0 ) వద్ద రెండవ ఉత్పన్నం , ఆ బిందువు రకాన్ని సూచిస్తుంది:

 

f '' ( x 0 )/ 0

 స్థానిక కనిష్ట

f '' ( x 0 ) <0

 స్థానిక గరిష్ట

f '' ( x 0 ) = 0

 నిర్ణయించబడలేదు

 

ఇది కూడ చూడు

కాలిక్యులస్
రాపిడ్ టేబుల్స్