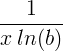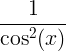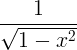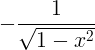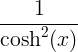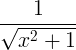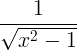مشتق اصول

اخذ کرنے والے اصول اور قوانین۔ افعال کی میز کے ماخوذ.

ماخوذ تعریف

جب فعل کا مشتق نقطہ x + Δx اور x withx کے ساتھ x کی افعال قدر f (x) کے فرق کا تناسب ہوتا ہے ، جب infx غیر معمولی طور پر چھوٹا ہوتا ہے۔ مشتق نقطہ X پر ٹینجینٹ لائن کی فنکشن ڈھلوان یا ڈھلوان ہے۔

 

f '(x) = \ لم _ _ \ \ ڈیلٹا x \ سے 0} \ frac {f (x + \ ڈیلٹا x) -f (x)} {\ ڈیلٹا x}

دوسرا مشتق

دوسرا ماخوذ از:

یا محض پہلی مشتق مشتق:

f '' (x) = (f '(x))'

Nth مشتق

ن ویں مشتق F (X) ن اوقات سمجھنے کی طرف سے شمار کیا جاتا ہے.

ن ویں مشتق ہے (N-1) مشتق مشتق کے برابر:

f ( n ) ( x ) = [ f ( n -1) ( x )] '

مثال:

کے چوتھے مشتق کو تلاش کریں

f ( x ) = 2 x 5

f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x

فعل کے گراف پر مشتق

کسی فعل سے ماخوذ ٹینجینٹل لائن کی ڈھلوان ہے۔

مشتق اصول

ماخوذ رقم کا قاعدہ

( اے ایف ( ایکس ) + بی جی ( ایکس )) '= اف' ( ایکس ) + بی جی ' ( ایکس )
مشتق مصنوع کا قاعدہ

( ایف ( ایکس ) ∙ جی ( ایکس )) '= ایف' ( ایکس ) جی ( ایکس ) + ایف ( ایکس ) جی ' ( ایکس )
ماخوذ قارئین اصول 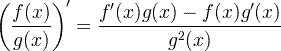\ بائیں (rac frac {f (x)} {g (x)} \ دائیں) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( ایکس)}
ماخوذ چین کا قاعدہ

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

ماخوذ رقم کا قاعدہ

جب ایک اور بی مستقل ہوتے ہیں۔

( اے ایف ( ایکس ) + بی جی ( ایکس )) '= اف' ( ایکس ) + بی جی ' ( ایکس )

مثال:

مشتق ڈھونڈیں:

3 ایکس 2 + 4 ایکس

مجموعی اصول کے مطابق:

a = 3 ، b = 4

f ( x ) = x 2 ، g ( x ) = x

f ' ( x ) = 2 x ، g' ( x ) = 1

(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

مشتق مصنوع کا قاعدہ

( ایف ( ایکس ) ∙ جی ( ایکس )) '= ایف' ( ایکس ) جی ( ایکس ) + ایف ( ایکس ) جی ' ( ایکس )

ماخوذ قارئین اصول

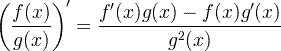
\ بائیں (rac frac {f (x)} {g (x)} \ دائیں) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( ایکس)}

ماخوذ چین کا قاعدہ

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

اس حکمنامے کو لیگرینج کے اشارے سے بہتر طور پر سمجھا جاسکتا ہے:

rac frac {df} {dx} = \ frac {df} g dg} d cdot \ frac {dg} {dx}

فنکشن لکیری لگ بھگ

چھوٹے Δx کے ل we ، جب ہم f (x 0 ) اور f '(x 0 ) جانتے ہیں تو ، ہم f (x 0 + Δx) کا قریب تر حاصل کرسکتے ہیں :

f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x

افعال کی میز کے ماخوذ

فنکشن کا نام فنکشن ماخوذ

f ( x )

 f '( x )
مستقل

const

0

لکیری

x

1

طاقت

x a

کلہاڑی a- 1
گستاخانہ

ای ایکس

ای ایکس
گستاخانہ

ایک ایکس

a x ln a
قدرتی لوگارڈم

ایل این ( ایکس )

لوگرتھم

لاگ B ( x )

سائن

sin x

کاکس x
کوسن

کاکس x

سن x
ٹینجینٹ

ٹین ایکس

آرکسین

آرکنسن x

آرکووسین

آرکاوس x

آرکٹینجینٹ

آرکٹان x
ہائپربولک سائن

sinh x

کوش ایکس
ہائپربولک کوسائن

کوش ایکس

sinh x
ہائپربولک ٹینجنٹ

تنہ x

الٹا ہائپربولک سائین

sinh -1 x

الٹا ہائپربولک کوسائن

کوش -1 ایکس

الٹا ہائپربولک ٹینجنٹ

تنہ -1 ایکس

مشتق مثالیں

مثال # 1

f ( x ) = x 3 +5 x 2 + x +8

f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1

مثال # 2

f ( x ) = sin (3 x 2 )

چین رول کو لاگو کرتے وقت:

f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = کیونکہ (3 x 2 ) ⋅ 6 x

دوسرا مشتق ٹیسٹ

جب کسی فنکشن کا پہلا مشتق نقطہ X 0 پر صفر ہوتا ہے ۔

f '( x 0 ) = 0

پھر نقطہ x 0 ، f '' (x 0 ) پر دوسرا مشتق ، اس نقطہ کی قسم کی نشاندہی کرسکتا ہے:

 

f '' ( x 0 )/ 0

 مقامی کم از کم

f '' ( x 0 ) <0

 مقامی زیادہ سے زیادہ

f '' ( x 0 ) = 0

 غیر متوقع

 

بھی دیکھو

کیلکولس
ریپڈ ٹیبلیاں