Сгъване
Конволюцията е корелационната функция на f (τ) с обърната функция g (t-τ).
Операторът на конволюцията е символът със звездичка * .
- Непрекъсната навивка
- Дискретна навивка
- 2D дискретна навивка
- Филтриране на изпълнение с конволюция
- Теорема за конволюцията
Непрекъсната навивка
Конволюцията на f (t) и g (t) е равна на интеграла от f (τ) по f (t-τ):
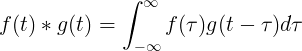
Дискретна навивка
Конволюцията на 2 дискретни функции се дефинира като:
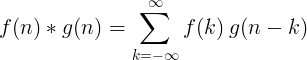
2D дискретна навивка
Двумерна дискретна навивка обикновено се използва за обработка на изображения.
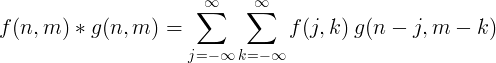
Филтриране на изпълнение с конволюция
Можем да филтрираме дискретния входен сигнал x (n) чрез конволюция с импулсната характеристика h (n), за да получим изходния сигнал y (n).
y ( n ) = x ( n ) * h ( n )
Теорема за конволюцията
Трансформацията на Фурие при умножение на 2 функции е равна на конволюцията на преобразуванията на Фурие на всяка функция:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
Преобразуването на Фурие на конволюция от 2 функции е равно на умножението на преобразуванията на Фурие на всяка функция:
ℱ { f * g } = ℱ { f } ⋅ ℱ { g }
Теорема за конволюцията за непрекъснато преобразуване на Фурие
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
Теорема за конволюцията за дискретно преобразуване на Фурие
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
Теорема за конволюцията за преобразуване на Лаплас
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )
Вижте също
КАЛКУЛ
- Ограничение
- Производно
- Неразделна
- Серия
- Лапласова трансформация
- Сгъване
- Символи за смятане
БЪРЗИ МАСИ