কনভলিউশন

রূপান্তর হ'ল বিপরীত ফাংশন জি (টি-with) এর সাথে চ (τ) এর সম্পর্কযুক্ত ফাংশন।

কনভোলশন অপারেটরটি হচ্ছে অ্যাসিড্রিক প্রতীক * ।

F (t) এবং g (t) এর কনভোলশন f (τ) বার f (t-τ) এর অবিচ্ছেদ্য সমান:

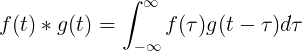
$f (t) * g (t) = \ int _ {- ty infty} ^ {\ infty} f (au tau) g (t- \ tau) d \ tau$

2 টি পৃথক ফাংশনের রূপান্তরটি সংজ্ঞায়িত করা হয়:

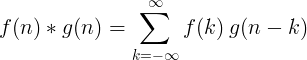
$f (n) * g (n) = \ sum_ {k = - \ infty} ^ {\ infty} f (k) \: g (nk)$

2 ডাইমেনশনাল ডিস্রিট কনভ্যুলেশন সাধারণত চিত্র প্রক্রিয়াকরণের জন্য ব্যবহৃত হয়।

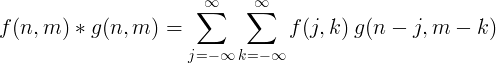
$f (n, m) * g (n, m) = \ Sum_ {j = - \ infty} ^ {\ infty} \ Sum_ {k = - \ infty} ^ {\ infty} f (j, k) \: ছ (এনজে, এমকে)$

আউটপুট সিগন্যাল y (n) পেতে আবেগ প্রতিক্রিয়া h (n) দিয়ে কনভলিউশনের মাধ্যমে আমরা আলাদা ইনপুট সিগন্যাল x (n) ফিল্টার করতে পারি।

y ( n ) = x ( n ) * h ( n )

2 ফাংশনের একটি গুণটির ফুরিয়ার রূপান্তর প্রতিটি ফাংশনের ফুরিয়ার রূপান্তরগুলির সমাবর্তনের সমান:

ℱ { চ ⋅ জি } = ℱ { এফ } * ℱ { জি }

2 ফাংশনগুলির একটি রূপান্তরটির ফুরিয়ার রূপান্তর প্রতিটি ফাংশনের ফুরিয়ার রূপান্তরগুলির গুণকের সমান:

ℱ { চ * জি } = ℱ { ফ } ⋅ ℱ { জি }

ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * জি ( ω )

ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )

ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = এফ ( কে ) * জি ( কে )

ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n ) F = এফ ( কে ) ⋅ জি ( কে )

ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( গুলি ) ⋅ জি ( গুলি )

আরো দেখুন