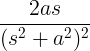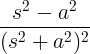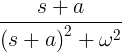ল্যাপ্লেস ট্রান্সফর্ম
- ল্যাপ্লেস রূপান্তর ফাংশন
- ল্যাপ্লেস রূপান্তর টেবিল
- ল্যাপ্লেস রূপান্তর বৈশিষ্ট্য
- ফলস্বরূপ উদাহরণ রূপান্তর
ল্যাপ্লেস শূন্য থেকে অনন্তে একীকরণের দ্বারা একটি সময় ডোমেন ফাংশনকে এস-ডোমেন ফাংশনে রূপান্তর করে
সময় ডোমেইন ফাংশনের, দ্বারা গুন ই -st ।
ল্যাপ্লেস ট্রান্সফর্মটি ডিফারেনশিয়াল সমীকরণ এবং ইন্টিগ্রালগুলির জন্য দ্রুত সমাধান সন্ধান করতে ব্যবহৃত হয়।
সময় ডোমেনের ব্যয়টি এস-ডোমেনে s দ্বারা গুণায় রূপান্তরিত হয়।
সময় ডোমেনের সংহতকরণগুলি এস-ডোমেনে বিভাগ দ্বারা রূপান্তরিত হয়।
ল্যাপ্লেস রূপান্তর ফাংশন
ল্যাপ্লেস ট্রান্সফর্মটি এল {} অপারেটরের সাথে সংজ্ঞায়িত করা হয় :
![]()
বিপরীত ল্যাপ্লেস রূপান্তর
বিপরীত ল্যাপ্লেস রূপান্তর সরাসরি গণনা করা যেতে পারে।
সাধারণত বিপরীত রূপান্তরটি রূপান্তর টেবিল থেকে দেওয়া হয়।
ল্যাপ্লেস রূপান্তর টেবিল
| ফাংশন নাম | সময় ডোমেন ফাংশন | ল্যাপ্লেস রূপান্তর |
|---|---|---|
চ ( টি ) |
F ( গুলি ) = L { f ( t ) |
|
| ধ্রুবক | 1 | |
| লিনিয়ার | t | |
| শক্তি | t এন |
|
| শক্তি | t a |
Γ ( a +1) - s - ( a +1) |
| উদ্দীপক | ই এ |
|
| সাইন | পাপ এ |
|
| কোসিন | কারণ এ |
|
| হাইপারবোলিক সাইন | sinh at |
|
| হাইপারবোলিক কোসাইন | কশ এ |
|
| সাইন বাড়ছে | T পাপ এ |
|
| বাড়ছে কোসাইন cos | টি কোসাইন্ এ |
|
| ক্ষয়কারী সাইন | ই -এ পাপ ωt |
|
| ক্ষয়িষ্ণু কোসাইন | ই -এ কোসাইন্ ωt |
|
| ডেল্টা ফাংশন | δ ( টি ) |
1 |
| বিলম্বিত ব-দ্বীপ | δ ( টা ) |
e -as |
ল্যাপ্লেস রূপান্তর বৈশিষ্ট্য
| সম্পত্তির নাম | সময় ডোমেন ফাংশন | ল্যাপ্লেস রূপান্তর | মন্তব্য |
|---|---|---|---|
চ ( টি ) |
এফ ( গুলি ) |
||
| লিনিয়ারিটি | আফ ( টি ) + বিজি ( টি ) | এএফ ( গুলি ) + বিজি ( গুলি ) | ক , খ ধ্রুবক |
| স্কেল পরিবর্তন | চ ( এ ) | |
a / 0 |
| শিফট | ই- এ্যাট এফ ( টি ) | এফ ( এস + এ ) | |
| বিলম্ব | চ ( টা ) | ই - যেমন এফ ( গুলি ) | |
| ডেরাইভেশন | |
এসএফ ( গুলি ) - চ (0) | |
| এন-থের উত্স | |
s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0) | |
| শক্তি | t n f ( t ) | |
|
| মিশ্রণ | |
|
|
| পারস্পরিক | |
|
|
| কনভলিউশন | f ( t ) * g ( t ) | এফ ( গুলি ) ⋅ জি ( গুলি ) | * কনভোলশন অপারেটর |
| পর্যায়ক্রমিক কাজ | f ( t ) = f ( t + T ) | |
ফলস্বরূপ উদাহরণ রূপান্তর
উদাহরণ # 1
চ (টি) এর রূপান্তরটি সন্ধান করুন:
f ( t ) = 3 টি + 2 টি 2
সমাধান:
ℒ { t } = 1 / s 2
{{ T 2 } = 2 / s 3
এফ ( গুলি ) = ℒ { চ ( টি )} = ℒ {3 টি + 2 টি 2 } = 3ℒ { টি } + 2ℒ { টি 2 } = 3 / এস 2 + 4 / এস 3
উদাহরণ # 2
F (গুলি) এর বিপরীত রূপান্তরটি সন্ধান করুন:
এফ ( গুলি ) = 3 / ( গুলি 2 + গুলি - 6)
সমাধান:
বিপরীত রূপান্তরটি খুঁজে পেতে, আমাদের ডোমেন ফাংশনটিকে একটি আরও সহজ আকারে পরিবর্তন করতে হবে:
এফ ( গুলি ) = 3 / ( এস 2 + এস - 6) = 3 / [( এস -2) ( এস +3)] = এ / ( এস -2) + বি / ( এস +3)
[ a ( s +3) + বি ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( গুলি +3)]
a ( s +3) + b ( s -2) = 3
একটি এবং খ খুঁজে পেতে, আমরা 2 টি সমীকরণ পেয়েছি - এর অন্যতম সহগ এবং বাকী দ্বিতীয়টি:
( a + b ) s + 3 a -2 খ = 3
a + b = 0, 3 এ -2 খ = 3
a = 3/5, b = -3/5
এফ ( গুলি ) = 3/5 ( গুলি -2) - 3/5 ( গুলি +3)
এখন F (গুলি) এক্সপোনেন্ট ফাংশনের জন্য ট্রান্সফর্ম টেবিলটি ব্যবহার করে সহজেই রূপান্তর করা যায়:
f ( t ) = (3/5) e 2 t - (3/5) e -3 t
আরো দেখুন
ক্যালকুলাস
- সীমাবদ্ধতা
- অমৌলিক
- ইন্টিগ্রাল
- সিরিজ
- ল্যাপ্লেস রূপান্তর
- কনভলিউশন
- ক্যালকুলাস প্রতীক
দ্রুত টেবিল