বৈচিত্র্য
সম্ভাবনা এবং পরিসংখ্যানগুলিতে, একটি এলোমেলো ভেরিয়েবলের বৈকল্পিক গড় মান থেকে বর্গ দূরত্বের গড় মান। এটি র্যান্ডম ভেরিয়েবলকে কীভাবে গড় মানের কাছে বিতরণ করা হয় তা উপস্থাপন করে। ছোট বৈকল্পিক ইঙ্গিত দেয় যে এলোমেলো পরিবর্তনশীল গড় মানের কাছাকাছি বিতরণ করা হয়। বড় বৈকল্পিক ইঙ্গিত দেয় যে এলোমেলো পরিবর্তনশীল গড় মান থেকে অনেক দূরে বিতরণ করা হয়। উদাহরণস্বরূপ, সাধারণ বিতরণ সহ, সংকীর্ণ বেল কার্ভের মধ্যে ছোট বৈকল্পিক থাকবে এবং প্রশস্ত বেল বক্ররেখাতে বড় বৈকল্পিক থাকবে।
ভেরিয়েন্স সংজ্ঞা
এলোমেলো ভেরিয়েবল এক্স এর বৈচিত্রটি এক্স এর পার্থক্যের স্কোয়ারের প্রত্যাশিত মান এবং প্রত্যাশিত মান μ μ
σ 2 = ভার ( এক্স ) = ই [( এক্স - μ ) 2 ]
পরিবর্তনের সংজ্ঞা থেকে আমরা পেতে পারি
σ 2 = ভার ( এক্স ) = ই ( এক্স 2 ) - μ 2
অবিচ্ছিন্ন র্যান্ডম ভেরিয়েবলের বৈকল্পিক
গড় মান with এবং সম্ভাবনার ঘনত্ব ফাংশন এফ (এক্স) সহ অবিচ্ছিন্ন র্যান্ডম ভেরিয়েবলের জন্য:
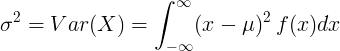
বা
![ভার (এক্স) = \ বাম [\ অন্তঃ _ {- ty ইনফটি} ^ {\ ইনফটি} x ^ 2 \: এফ (এক্স) ডেক্স \ ডান] - \ মিউ ^ 2](variance/cont_var2.gif)
বিচ্ছিন্ন র্যান্ডম ভেরিয়েবলের বৈকল্পিক
গড় মান disc এবং সম্ভাব্য ভর ফাংশন পি (এক্স) সহ বিচ্ছিন্ন র্যান্ডম ভেরিয়েবল এক্সের জন্য:
![]()
বা
![বর্ণ (এক্স) = \ বাম [\ যোগ_ {i} ^ {} x_i ^ 2 পি (x_i) \ ডান] - \ মিউ 2](variance/disc_var2.gif)
বৈকল্পিক বৈশিষ্ট্য
যখন এক্স এবং ওয়াই স্বতন্ত্র এলোমেলো পরিবর্তনশীল:
ভার ( এক্স + ওয়াই ) = ভার ( এক্স ) + ভার ( ওয়াই )
আরো দেখুন
সম্ভাব্যতা ও পরিসংখ্যান
- প্রাথমিক সম্ভাবনা prob
- প্রত্যাশা
- বৈচিত্র্য
- আদর্শ বিচ্যুতি
- সম্ভাবনা বিতরণ
- স্বাভাবিক বন্টন
- পরিসংখ্যান প্রতীক
দ্রুত টেবিল