Convolució
La convolució és la funció de correlació de f (τ) amb la funció invertida g (t-τ).
L'operador de convolució és el símbol de l'asterisc * .
- Convolució contínua
- Convolució discreta
- Convolució discreta 2D
- Implementació de filtres amb convolució
- Teorema de la convolució
Convolució contínua
La convolució de f (t) i g (t) és igual a la integral de f (τ) vegades f (t-τ):
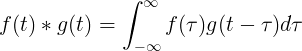
Convolució discreta
La convolució de 2 funcions discretes es defineix com:
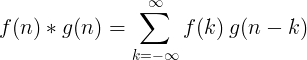
Convolució discreta 2D
La convolució discreta bidimensional s'utilitza generalment per al processament d'imatges.
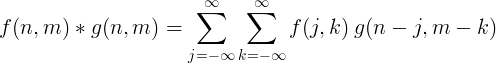
Implementació de filtres amb convolució
Podem filtrar el senyal d’entrada discret x (n) per convolució amb la resposta d’impuls h (n) per obtenir el senyal de sortida y (n).
y ( n ) = x ( n ) * h ( n )
Teorema de la convolució
La transformada de Fourier d’una multiplicació de 2 funcions és igual a la convolució de les transformades de Fourier de cada funció:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
La transformada de Fourier d'una convolució de 2 funcions és igual a la multiplicació de les transformades de Fourier de cada funció:
ℱ { f * g } = ℱ { f } ⋅ ℱ { g }
Teorema de la convolució per a la transformada de Fourier contínua
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
Teorema de la convolució per a la transformada de Fourier discreta
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
Teorema de la convolució per a la transformada de Laplace
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )
Vegeu també
CÀLCUL
- Límit
- Derivada
- Integral
- Sèrie
- Transformada de Laplace
- Convolució
- Símbols de càlcul
TAULES RÀPIDES