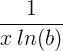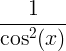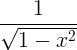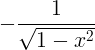Regles derivades

Normes i lleis derivades. Taula de derivades de funcions.

Definició derivada

La derivada d'una funció és la proporció de la diferència del valor de la funció f (x) en els punts x + Δx i x amb Δx, quan Δx és infinitesimalment petit. La derivada és la funció pendent o pendent de la recta tangent en el punt x.

 

f '(x) = \ lim _ {\ Delta x \ to 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}

Segona derivada

La segona derivada ve donada per:

O simplement derivar la primera derivada:

f '' (x) = (f '(x))'

Enèsima derivada

El n º derivada es calcula mitjançant la derivació de f (x) n vegades.

Els n TH derivada igual a la derivada de la (n-1) derivat de:

f ( n ) ( x ) = [ f ( n -1) ( x )] '

Exemple:

Troba la quarta derivada de

f ( x ) = 2 x 5

f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x

Derivada en el gràfic de funció

La derivada d’una funció és la inclinació de la línia tangencial.

Regles derivades

Regla de suma derivada

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Regla de producte derivat

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Regla del quocient derivat 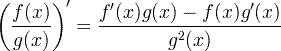\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}
Regla de cadena de derivats

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Regla de suma derivada

Quan a i b són constants.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Exemple:

Trobeu la derivada de:

3 x 2 + 4 x.

Segons la regla de suma:

a = 3, b = 4

f ( x ) = x 2 , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Regla de producte derivat

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Regla del quocient derivat

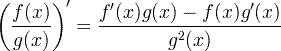
\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}

Regla de cadena de derivats

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Aquesta regla es pot entendre millor amb la notació de Lagrange:

\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}

Funció aproximació lineal

Per a Δx petit, podem obtenir una aproximació a f (x 0 + Δx), quan sabem f (x 0 ) i f '(x 0 ):

f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x

Taula de derivades de funcions

Nom de la funció Funció Derivada

f ( x )

 f '( x )
Constant

const

0

Lineal

x

1

Potència

x a

destral a- 1
Exponencial

e x

e x
Exponencial

una x

a x ln a
Logaritme natural

ln ( x )

Logaritme

registre b ( x )

Sinus

pecat x

cos x
Cosinus

cos x

-sin x
Tangent

tan x

Arcsine

arcsin x

Arccosina

arccos x

Arctangent

arctan x
Sinus hiperbòlic

sinh x

cosh x
Cosinus hiperbòlic

cosh x

sinh x
Tangent hiperbòlica

tanh x

Sinus hiperbòlic invers

sinh -1 x

Cosinus hiperbòlic invers

cosh -1 x

Tangent hiperbòlica inversa

tanh -1 x

Exemples derivats

Exemple 1

f ( x ) = x 3 +5 x 2 + x +8

f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1

Exemple 2

f ( x ) = sin (3 x 2 )

Quan apliqueu la regla de la cadena:

f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x

Segona prova derivada

Quan la primera derivada d’una funció és zero en el punt x 0 .

f '( x 0 ) = 0

A continuació, la segona derivada en el punt x 0 , f "(x 0 ), pot indicar el tipus d'aquest punt:

 

f "( x 0 )/ 0

 mínim local

f "( x 0 ) <0

 màxim local

f "( x 0 ) = 0

 indeterminat

 

Vegeu també

CÀLCUL
TAULES RÀPIDES