Fórmules bàsiques de probabilitat

 

Rang de probabilitats

0 ≤ P ( A ) ≤ 1

Regla d’esdeveniments complementaris

P ( A C ) + P ( A ) = 1

Regla d'addició

P (A∪B) = P (A) + P (B) - P (A∩B)

Esdeveniments disjunts

Els esdeveniments A i B són si disjunts

P (A∩B) = 0

Probabilitat condicional

P (A | B) = P (A∩B) / P (B)

Fórmula Bayes

P (A | B) = P (B | A) ⋅ P (A) / P (B)

Esdeveniments independents

Els esdeveniments A i B són independents si no

P (A∩B) = P (A) ⋅ P (B)

Funció de distribució acumulativa

F X ( x ) = P ( X ≤ x )

Funció de massa de probabilitat

suma (i = 1..n, P (X = x (i)) = 1

Funció de densitat de probabilitat

fX (x) = dFX (x) / dx

FX (x) = integral (-inf..x, fX (y) * dy)

FX (x) = suma (k = 1..x, P (X = k))

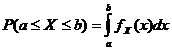
P (a <= X <= b) = integral (a..b, fX (x) * dx)

integral (-inf..inf, fX (x) * dx) = 1

 

Covariància

Cox (X, Y) = E (X-ux) (Y-uy) = E (XY) - ux * uy

Correlació

corr (X, Y) = Cov (X, Y) / (Std (X) * Std (Y))

 

Bernoulli: 0-fracàs 1-èxit

Geomètric: 0-fracàs 1-èxit

Hipergeomètric: es prenen N objectes amb K objectes d’èxit, es prenen n objectes.

 

 

 
 
PROBABILITAT I ESTADÍSTICA
TAULES RÀPIDES