Kvadratisk ligning
Kvadratisk ligning er et andet ordens polynom med 3 koefficienter - a , b , c .
Den kvadratiske ligning er givet ved:
økse 2 + bx + c = 0
Løsningen på den kvadratiske ligning er givet med 2 tal x 1 og x 2 .
Vi kan ændre den kvadratiske ligning til form af:
( x - x 1 ) ( x - x 2 ) = 0
Kvadratisk formel
Løsningen på den kvadratiske ligning er givet ved den kvadratiske formel:
![]()
Udtrykket inde i kvadratroden kaldes diskriminerende og betegnes med Δ:
Δ = b 2 - 4 ac
Den kvadratiske formel med diskriminerende notation:
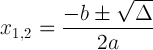
Dette udtryk er vigtigt, fordi det kan fortælle os om løsningen:
- Når Δ/ 0, er der 2 reelle rødder x 1 = (- b + √ Δ ) / (2a) og x 2 = (- b-√ Δ ) / (2a) .
- Når Δ = 0, er der en rod x 1 = x 2 = -b / (2a) .
- Når Δ <0, er der ingen reelle rødder, der er 2 komplekse rødder:
x 1 = (- b + i√ -Δ ) / (2a) og x 2 = (- bi√ -Δ ) / (2a) .
Problem nr. 1
3 x 2 +5 x +2 = 0
løsning:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Problem nr.2
3 x 2 -6 x 3 = 0
løsning:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Problem nr.3
x 2 +2 x +5 = 0
løsning:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Der er ingen reelle løsninger. Værdierne er komplekse tal:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Kvadratisk funktionsgraf
Den kvadratiske funktion er en anden ordens polynomfunktion:
f ( x ) = ax 2 + bx + c
Løsningerne til den kvadratiske ligning er rødderne til den kvadratiske funktion, det vil sige skæringspunkterne for den kvadratiske funktionsgraf med x-aksen, når
f ( x ) = 0
Når der er to skæringspunkter i grafen med x-aksen, er der 2 løsninger på den kvadratiske ligning.
Når der er 1 skæringspunkt i grafen med x-aksen, er der 1 løsning på den kvadratiske ligning.
Når der ikke er nogen skæringspunkter i grafen med x-aksen, får vi ikke rigtige løsninger (eller 2 komplekse løsninger).