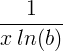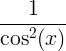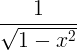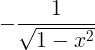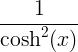Afledte regler
Afledte regler og love. Afledte af funktionstabel.
Derivat definition
Den afledte af en funktion er forholdet mellem forskellen i funktionsværdien f (x) i punkterne x + Δx og x med Δx, når Δx er uendelig lille. Derivatet er funktionshældningen eller hældningen af tangentlinjen ved punkt x.
![]()
Andet afledt
Det andet derivat er givet af:
![]()
Eller udled blot det første derivat:
![]()
Niende derivat
Den n th derivat beregnes ved at udlede f (x) n gange.
Det n -derivat er lig med derivatet af (n-1) -derivatet:
f ( n ) ( x ) = [ f ( n -1) ( x )] '
Eksempel:
Find det fjerde afledte af
f ( x ) = 2 x 5
f (4) ( x ) = [2 x 5 ] '' '[10 x 4 ]' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x
Afledt på graf af funktion
Den afledte af en funktion er skråningen af den tangentielle linje.
Afledte regler
| Derivatregel | ( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x ) |
| Derivatregel | ( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x ) |
| Afledt kvotientregel | 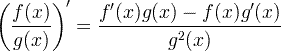 |
| Derivat kæde regel | f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x ) |
Derivatregel
Når a og b er konstanter.
( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Eksempel:
Find afledningen af:
3 x 2 + 4 x.
Ifølge sumreglen:
a = 3, b = 4
f ( x ) = x 2 , g ( x ) = x
f ' ( x ) = 2 x , g' ( x ) = 1
(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4
Derivatregel
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Afledt kvotientregel
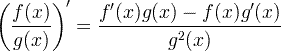
Derivat kæde regel
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )
Denne regel kan bedre forstås med Lagrange's notation:
![]()
Funktion lineær tilnærmelse
For lille Δx kan vi få en tilnærmelse til f (x 0 + Δx), når vi kender f (x 0 ) og f '(x 0 ):
f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x
Afledte af funktionstabel
| Funktionsnavn | Fungere | Afledte |
|---|---|---|
| f ( x ) |
f '( x ) | |
| Konstant | konst |
0 |
| Lineær | x |
1 |
| Strøm | x a |
økse a- 1 |
| Eksponentiel | e x |
e x |
| Eksponentiel | a x |
a x ln a |
| Naturlig logaritme | ln ( x ) |
|
| Logaritme | log b ( x ) |
|
| Sinus | synd x |
cos x |
| Cosine | cos x |
-sin x |
| Tangent | tan x |
|
| Arcsine | bueform x |
|
| Arccosine | arccos x |
|
| Arktangent | arctan x |
|
| Hyperbolisk sinus | sinh x |
cosh x |
| Hyperbolisk cosinus | cosh x |
sinh x |
| Hyperbolsk tangens | tanh x |
|
| Invers hyperbolsk sinus | sinh -1 x |
|
| Omvendt hyperbolsk cosinus | cosh -1 x |
|
| Omvendt hyperbolsk tangens | tanh -1 x |
|
Afledte eksempler
Eksempel nr. 1
f ( x ) = x 3 +5 x 2 + x +8
f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1
Eksempel 2
f ( x ) = sin (3 x 2 )
Ved anvendelse af kædereglen:
f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x
Anden afledt test
Når det første afledte af en funktion er nul ved punktet x 0 .
f '( x 0 ) = 0
Derefter kan det andet afledte ved punkt x 0 , f '' (x 0 ) angive typen af det punkt:
| f '' ( x 0 )/ 0 |
lokalt minimum |
| f '' ( x 0 ) <0 |
lokalt maksimum |
| f '' ( x 0 ) = 0 |
ubestemt |
Se også
KALKULUS
- Begrænse
- Afledte
- Integreret
- Serie
- Laplace-transformation
- Konvolution
- Calculus symboler
HUKyLabsIGE TABLER