Faltung
Die Faltung ist die Korrelationsfunktion von f (τ) mit der Umkehrfunktion g (t-τ).
Der Faltungsoperator ist das Sternsymbol * .
- Kontinuierliche Faltung
- Diskrete Faltung
- 2D diskrete Faltung
- Filterimplementierung mit Faltung
- Faltungssatz
Kontinuierliche Faltung
Die Faltung von f (t) und g (t) ist gleich dem Integral von f (τ) mal f (t-τ):
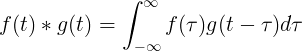
Diskrete Faltung
Die Faltung von 2 diskreten Funktionen ist definiert als:
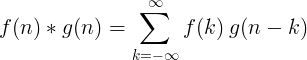
2D diskrete Faltung
Für die Bildverarbeitung wird üblicherweise eine zweidimensionale diskrete Faltung verwendet.
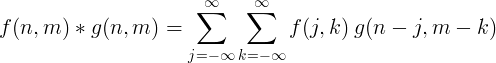
Filterimplementierung mit Faltung
Wir können das diskrete Eingangssignal x (n) durch Faltung mit der Impulsantwort h (n) filtern, um das Ausgangssignal y (n) zu erhalten.
y ( n ) = x ( n ) · h ( n )
Faltungssatz
Die Fourier-Transformation einer Multiplikation von 2 Funktionen ist gleich der Faltung der Fourier-Transformationen jeder Funktion:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
Die Fourier-Transformation einer Faltung von 2 Funktionen ist gleich der Multiplikation der Fourier-Transformationen jeder Funktion:
ℱ { f * g } = ℱ { f } ⋅ ⋅ { g }
Faltungssatz für die kontinuierliche Fourier-Transformation
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ⋅ { g ( t )} = F ( ω ) ⋅ G ( ω )
Faltungssatz für die diskrete Fourier-Transformation
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ⋅ { g ( n )} = F ( k ) ⋅ G ( k )
Faltungssatz für die Laplace-Transformation
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ⋅ { g ( t )} = F ( s ) ⋅ G ( s )
Siehe auch
INFINITESIMALRECHNUNG
- Grenze
- Derivat
- Integral
- Serie
- Laplace-Transformation
- Faltung
- Kalkülsymbole
SCHNELLE TABELLEN