Τετραγωνική εξίσωση
Η τετραγωνική εξίσωση είναι ένα πολυώνυμο δεύτερης τάξης με 3 συντελεστές - a , b , c .
Η τετραγωνική εξίσωση δίνεται από:
ax 2 + bx + c = 0
Η λύση στην τετραγωνική εξίσωση δίνεται από 2 αριθμούς x 1 και x 2 .
Μπορούμε να αλλάξουμε την τετραγωνική εξίσωση στη μορφή:
( x - x 1 ) ( x - x 2 ) = 0
Τετραγωνικός τύπος
Η λύση στην τετραγωνική εξίσωση δίνεται από τον τετραγωνικό τύπο:
![]()
Η έκφραση μέσα στην τετραγωνική ρίζα ονομάζεται διακριτική και συμβολίζεται με Δ:
Δ = b 2 - 4 ac
Ο τετραγωνικός τύπος με διακριτική σημειογραφία:
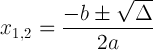
Αυτή η έκφραση είναι σημαντική επειδή μπορεί να μας πει για τη λύση:
- Όταν Δ/ 0, υπάρχουν 2 πραγματικές ρίζες x 1 = (- b + √ Δ ) / (2a) και x 2 = (- b-√ Δ ) / (2a) .
- Όταν Δ = 0, υπάρχει μία ρίζα x 1 = x 2 = -b / (2a) .
- Όταν Δ <0, δεν υπάρχουν πραγματικές ρίζες, υπάρχουν 2 σύνθετες ρίζες:
x 1 = (- b + i√ -Δ ) / (2a) και x 2 = (- bi√ -Δ ) / (2a) .
Πρόβλημα # 1
3 x 2 +5 x +2 = 0
λύση:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Πρόβλημα # 2
3 x 2 -6 x +3 = 0
λύση:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Πρόβλημα # 3
x 2 +2 x +5 = 0
λύση:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Δεν υπάρχουν πραγματικές λύσεις. Οι τιμές είναι σύνθετοι αριθμοί:
x 1 = -1 + 2 θ
x 2 = -1 - 2 θ
Γράφημα τετραγωνικής λειτουργίας
Η τετραγωνική συνάρτηση είναι μια πολυώνυμη συνάρτηση δεύτερης τάξης:
f ( x ) = ax 2 + bx + c
Οι λύσεις για την τετραγωνική εξίσωση είναι οι ρίζες της τετραγωνικής συνάρτησης, που είναι τα σημεία τομής του γραφήματος τετραγωνικής συνάρτησης με τον άξονα x, όταν
f ( x ) = 0
Όταν υπάρχουν 2 σημεία τομής του γραφήματος με τον άξονα x, υπάρχουν 2 λύσεις για την τετραγωνική εξίσωση.
Όταν υπάρχει 1 σημείο τομής του γραφήματος με τον άξονα x, υπάρχει 1 λύση στην τετραγωνική εξίσωση.
Όταν δεν υπάρχουν σημεία τομής του γραφήματος με τον άξονα x, δεν έχουμε πραγματικές λύσεις (ή 2 σύνθετες λύσεις).