Φυσικός λογάριθμος - ln (x)
Ο φυσικός λογάριθμος είναι ο λογάριθμος στη βάση e ενός αριθμού.
- Ορισμός φυσικού λογάριθμου (ln)
- Κανόνες και ιδιότητες φυσικού λογάριθμου (ln)
- Πολύπλοκος λογάριθμος
- Γράφημα του ln (x)
- Πίνακας φυσικών λογαρίθμων (ln)
- Υπολογιστής φυσικού λογάριθμου
Ορισμός του φυσικού λογάριθμου
Πότε
e y = x
Στη συνέχεια, ο βασικός λογάριθμος του x είναι
ln ( x ) = log e ( x ) = y
Η σταθερά e ή ο αριθμός Euler είναι:
ε ≈ 2.71828183
Ln ως αντίστροφη συνάρτηση της εκθετικής συνάρτησης
Η φυσική συνάρτηση λογάριθμου ln (x) είναι η αντίστροφη συνάρτηση της εκθετικής συνάρτησης e x .
Για x/ 0,
f ( f -1 ( x )) = e ln ( x ) = x
Ή
f -1 ( f ( x )) = ln ( e x ) = x
Κανόνες και ιδιότητες φυσικού λογάριθμου
| Όνομα κανόνα | Κανόνας | Παράδειγμα |
|---|---|---|
Κανόνας προϊόντος |
ln ( x ∙ y ) = ln ( x ) + ln ( y ) |
ln (3 ∙ 7) = ln (3) + ln (7) |
Ποσοτικός κανόνας |
ln ( x / y ) = ln ( x ) - ln ( y ) |
ln (3 / 7) = ln (3) - ln (7) |
Κανόνας ισχύος |
ln ( x y ) = y ∙ ln ( x ) |
ln (2 8 ) = 8 ∙ ln (2) |
Παράγωγο |
f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x | |
Αναπόσπαστο |
∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C | |
αρνητικό αριθμό |
Το ln ( x ) είναι απροσδιόριστο όταν x ≤ 0 | |
Στο μηδέν |
Το ln (0) είναι απροσδιόριστο | |
σε ένα |
ln (1) = 0 | |
Στο άπειρο |
lim ln ( x ) = ∞, όταν x → ∞ | |
| Η ταυτότητα του Euler | ln (-1) = i π |
Κανόνας προϊόντος λογάριθμου
Ο λογάριθμος του πολλαπλασιασμού των x και y είναι το άθροισμα του λογάριθμου του x και του λογάριθμου του y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Για παράδειγμα:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Κανόνας πηλίκου λογαρίθμου
Ο λογάριθμος της διαίρεσης των x και y είναι η διαφορά του λογάριθμου του x και του λογάριθμου του y.
log b ( x / y ) = log b ( x ) - log b ( y )
Για παράδειγμα:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Κανόνας ισχύος λογάριθμου
Ο λογάριθμος του x που αυξάνεται στη δύναμη του y είναι y φορές ο λογάριθμος του x.
log b ( x y ) = y ∙ log b ( x )
Για παράδειγμα:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Παράγωγο του φυσικού λογάριθμου
Το παράγωγο της συνάρτησης φυσικού λογάριθμου είναι η αμοιβαία συνάρτηση.
Πότε
f ( x ) = ln ( x )
Το παράγωγο του f (x) είναι:
f ' ( x ) = 1 / x
Ολοκληρωμένο φυσικό λογάριθμο
Το ολοκλήρωμα της συνάρτησης φυσικού λογάριθμου δίνεται από:
Πότε
f ( x ) = ln ( x )
Το ολοκλήρωμα του f (x) είναι:
∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C
Ln από 0
Ο φυσικός λογάριθμος του μηδέν είναι απροσδιόριστος:
Το ln (0) είναι απροσδιόριστο
Το όριο κοντά στο 0 του φυσικού λογάριθμου του x, όταν το x πλησιάζει το μηδέν, είναι μείον άπειρο:
![]()
Ln από 1
Ο φυσικός λογάριθμος ενός είναι μηδέν:
ln (1) = 0
Το άπειρο
Το όριο του φυσικού λογάριθμου του άπειρου, όταν το x πλησιάζει το άπειρο είναι ίσο με το άπειρο:
lim ln ( x ) = ∞, όταν x → ∞
Πολύπλοκος λογάριθμος
Για τον σύνθετο αριθμό z:
z = re iθ = x + iy
Ο σύνθετος λογάριθμος θα είναι (n = ...- 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
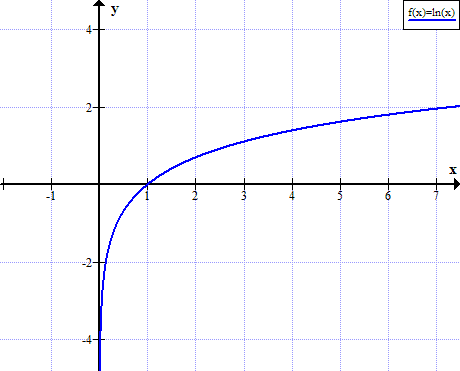
Γράφημα του ln (x)
Το ln (x) δεν ορίζεται για πραγματικές μη θετικές τιμές του x:
Πίνακας φυσικών λογαρίθμων
| x | στο x |
|---|---|
| 0 | απροσδιόριστος |
| 0 + | - ∞ |
| 0,0001 | -9.210340 |
| 0,001 | -6.907755 |
| 0,01 | -4.605170 |
| 0.1 | -2.302585 |
| 1 | 0 |
| 2 | 0,669147 |
| ε ≈ 2.7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1.791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5.991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1000 | 6.907755 |
| 10000 | 9.210340 |
Δείτε επίσης
- Λογάριθμος (ημερολόγιο)
- Υπολογιστής φυσικού λογάριθμου
- Φυσικός λογάριθμος μηδέν
- Φυσικός λογάριθμος ενός
- Φυσικός λογάριθμος του e
- Φυσικός λογάριθμος του απείρου
- Φυσικός λογάριθμος αρνητικού αριθμού
- Ln αντίστροφη συνάρτηση
- ln (x) γράφημα
- Πίνακας φυσικού λογάριθμου
- Αριθμομηχανή λογάριθμου
- ε σταθερά
ΑΛΓΕΒΡΑ
ΓΡΗΓΟΡΑ ΠΙΝΑΚΕΣ