Integraali

Integraatio on johdon käänteinen operaatio.

Funktion integraali on funktion kuvaajan alla oleva alue.

Määrittelemätön kokonaismääritelmä

Kun dF (x) / dx = f (x) =/ integraali (f (x) * dx) = F (x) + c

Määrittelemättömät kiinteät ominaisuudet

integraali (f (x) + g (x)) * dx = integraali (f (x) * dx) + integraali (g (x) * dx)

integraali (a * f (x) * dx) = a * integraali (f (x) * dx)

integraali (f (a * x) * dx) = 1 / a * F (a * x) + c

integraali (f (x + b) * dx) = F (x + b) + c

integraali (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

integraali (df (x) / dx * dx) = f (x)

Integraatiomuuttujan muutos

Kunx = g (t) jadx = g '(t) * dt

integraali (f (x) * dx) = integraali (f (g (t)) * g '(t) * dt)

Integrointi osittain

integraali (f (x) * g '(x) * dx) = f (x) * g (x) - integraali (f' (x) * g (x) * dx)

Integraalitaulukko

integraali (f (x) * dx = F (x) + c

integraali (a * dx) = a * x + c

integraali (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, kun a </ - 1

integraali (1 / x * dx) = ln (abs (x)) + c

integraali (e ^ x * dx) = e ^ x + c

integraali (a ^ x * dx) = a ^ x / ln (x) + c

integraali (ln (x) * dx) = x * ln (x) - x + c

integraali (sin (x) * dx) = -cos (x) + c

integraali (cos (x) * dx) = sin (x) + c

integraali (tan (x) * dx) = -ln (abs (cos (x))) + c

integraali (arcsin (x) * dx) = x * arcsin (x) + sqrt (1-x ^ 2) + c

integraali (arccos (x) * dx) = x * arccos (x) - sqrt (1-x ^ 2) + c

integraali (arctan (x) * dx) = x * arctan (x) - 1/2 * ln (1 + x ^ 2) + c

integraali (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

integraali (1 / sqrt (a ^ 2-x ^ 2) * dx) = arcsin (x / a) + c

integraali (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

integraali (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

integraali (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * arctan (x / a) + c

integraali (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

integraali (sinh (x) * dx) = cosh (x) + c

integraali (cosh (x) * dx) = sinh (x) + c

integraali (tanh (x) * dx) = ln (cosh (x)) + c

 

Selkeä kiinteä määritelmä

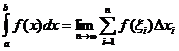
integraali (a..b, f (x) * dx) = lim (n-/ inf, summa (i = 1..n, f (z (i)) * dx (i))) 

Kunx0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

Selkeä integraalilaskenta

Kun ,

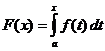 dF (x) / dx = f (x) ja

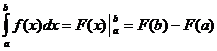
integraali (a..b, f (x) * dx) = F (b) - F (a) 

Selvät kiinteät ominaisuudet

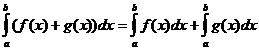
integraali (a..b, (f (x) + g (x)) * dx) = integraali (a..b, f (x) * dx) + integraali (a..b, g (x) * dx )

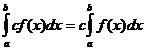
integraali (a..b, c * f (x) * dx) = c * integraali (a..b, f (x) * dx)

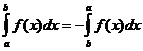
integraali (a..b, f (x) * dx) = - integraali (b..a, f (x) * dx)

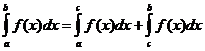
integraali (a..b, f (x) * dx) = integraali (a..c, f (x) * dx) + integraali (c..b, f (x) * dx)

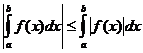
abs (integraali (a..b, f (x) * dx)) <= integraali (a..b, abs (f (x)) * dx)

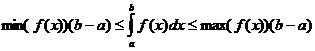min (f (x)) * (ba) <= integraali (a..b, f (x) * dx) <= max (f (x)) * (ba) kunx jäsen [a, b]

Integraatiomuuttujan muutos

Kunx = g (t) ,dx = g '(t) * dt ,g (alfa) = a ,g (beeta) = b

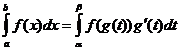
integraali (a..b, f (x) * dx) = integraali (alfa..beta, f (g (t)) * g '(t) * dt)

Integrointi osittain

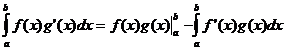
integraali (a..b, f (x) * g '(x) * dx) = integraali (a..b, f (x) * g (x) * dx) - integraali (a..b, f' (x) * g (x) * dx)

Keskiarvolause

Kun f ( x ) on jatkuva, on pistec on ryhmän [a, b] jäsen niin

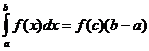
integraali (a..b, f (x) * dx) = f (c) * (ba)  

Määritetyn integraalin puolisuunnikkainen lähentäminen

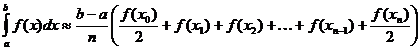
integraali (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

Gamma-toiminto

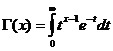
gamma (x) = integraali (0..inf, t ^ (x-1) * e ^ (- t) * dt

Gammatoiminto on konvergentti x/ 0: lle .

Gammatoiminnon ominaisuudet

G ( x +1) = x G ( x )

G ( n +1) = n ! , kun n ℕ (positiivinen kokonaisluku).on jäsenenä

Beetatoiminto

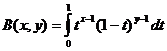
B (x, y) = integraali (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

Beetatoiminnon ja gammafunktion suhde

B (x, y) = Gamma (x) * Gamma (y) / Gamma (x + y)

 

 

 

LASKU
NOPEAT PÖYTÄT