Équation quadratique
L'équation quadratique est un polynôme du second ordre avec 3 coefficients - a , b , c .
L'équation quadratique est donnée par:
hache 2 + bx + c = 0
La solution de l'équation quadratique est donnée par 2 nombres x 1 et x 2 .
Nous pouvons changer l'équation quadratique sous la forme de:
( x - x 1 ) ( x - x 2 ) = 0
Formule quadratique
La solution de l'équation quadratique est donnée par la formule quadratique:
![]()
L'expression à l'intérieur de la racine carrée est appelée discriminante et est notée Δ:
Δ = b deux - quatre ac
La formule quadratique avec notation discriminante:
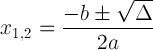
Cette expression est importante car elle peut nous renseigner sur la solution:
- Lorsque Δ/ 0, il y a 2 racines réelles x 1 = (- b + √ Δ ) / (2a) et x 2 = (- b-√ Δ ) / (2a) .
- Lorsque Δ = 0, il y a une racine x 1 = x 2 = -b / (2a) .
- Lorsque Δ <0, il n'y a pas de racines réelles, il y a 2 racines complexes:
x 1 = (- b + i√ -Δ ) / (2a) et x 2 = (- bi√ -Δ ) / (2a) .
Problème n ° 1
3 x 2 +5 x +2 = 0
Solution:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Problème n ° 2
3 x 2 -6 x +3 = 0
Solution:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Problème n ° 3
x 2 +2 x +5 = 0
Solution:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Il n'y a pas de vraies solutions. Les valeurs sont des nombres complexes:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Graphique de fonction quadratique
La fonction quadratique est une fonction polynomiale du second ordre:
f ( x ) = ax 2 + bx + c
Les solutions de l'équation quadratique sont les racines de la fonction quadratique, qui sont les points d'intersection du graphe de fonction quadratique avec l'axe des x, lorsque
f ( x ) = 0
Lorsqu'il y a 2 points d'intersection du graphique avec l'axe des x, il y a 2 solutions à l'équation quadratique.
Lorsqu'il y a 1 point d'intersection du graphique avec l'axe des x, il y a 1 solution à l'équation quadratique.
Lorsqu'il n'y a pas de points d'intersection du graphe avec l'axe des x, nous n'obtenons pas de vraies solutions (ou 2 solutions complexes).