Règles de logarithme

Le logarithme de base b d'un nombre est l' exposant dont nous avons besoin pour élever la base afin d'obtenir le nombre.

Définition du logarithme

Lorsque b est élevé à la puissance y est égal à x:

b y = x

Alors le logarithme de base b de x est égal à y:

log b ( x ) = y

Par exemple quand:

2 4 = 16

ensuite

log 2 (16) = 4

Logarithme comme fonction inverse de la fonction exponentielle

La fonction logarithmique,

y = log b ( x )

est la fonction inverse de la fonction exponentielle,

x = b y

Donc, si nous calculons la fonction exponentielle du logarithme de x (x/ 0),

f ( f -1 ( x )) = b log b ( x ) = x

Ou si nous calculons le logarithme de la fonction exponentielle de x,

f -1 ( f ( x )) = log b ( b x ) = x

Logarithme naturel (ln)

Le logarithme naturel est un logarithme de la base e:

ln ( x ) = log e ( x )

Quand e constante est le nombre:

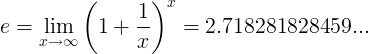
e = \ lim_ {x \ rightarrow \ infty} \ left (1+ \ frac {1} {x} \ right) ^ x = 2,718281828459 ...

ou

e = \ lim_ {x \ rightarrow 0} \ left (1+ \ right x) ^ \ frac {1} {x}

 

Voir: Logarithme naturel

Calcul du logarithme inverse

Le logarithme inverse (ou anti logarithme) est calculé en élevant la base b au logarithme y:

x = log -1 ( y ) = b y

Fonction logarithmique

La fonction logarithmique a la forme de base de:

f ( x ) = log b ( x )

Règles de logarithme

Nom de la règle Règle
Règle de produit logarithmique
 log b ( x ∙ y ) = log b ( x ) + log b ( y )
Règle du quotient logarithmique
 log b ( x / y ) = log b ( x ) - log b ( y )
Règle de puissance logarithmique
 log b ( x y ) = y ∙ log b ( x )
Règle de commutation de base logarithmique
 log b ( c ) = 1 / log c ( b )
Règle de changement de base du logarithme
 log b ( x ) = log c ( x ) / log c ( b )
Dérivée du logarithme
 f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b ))
Intégrale du logarithme
 ∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
Logarithme du nombre négatif
 log b ( x ) n'est pas défini lorsque x ≤ 0
Logarithme de 0
 log b (0) n'est pas défini
\ lim_ {x \ to 0 ^ +} \ textup {log} _b (x) = - \ infty
Logarithme de 1
 log b (1) = 0
Logarithme de la base
 log b ( b ) = 1
Logarithme de l'infini
 lim log b ( x ) = ∞, lorsque x → ∞

Voir: Règles de logarithme

 

Règle de produit logarithmique

Le logarithme de la multiplication de x et y est la somme du logarithme de x et du logarithme de y.

log b ( x ∙ y ) = log b ( x ) + log b ( y )

Par exemple:

log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)

Règle du quotient logarithmique

Le logarithme de la division de x et y est la différence du logarithme de x et du logarithme de y.

log b ( x / y ) = log b ( x ) - log b ( y )

Par exemple:

log 10 (3 / 7) = log 10 (3) - log 10 (7)

Règle de puissance logarithmique

Le logarithme de x élevé à la puissance y est y fois le logarithme de x.

log b ( x y ) = y ∙ log b ( x )

Par exemple:

log 10 (2 8 ) = 8 ∙ log 10 (2)

Règle de commutation de base logarithmique

Le logarithme de base b de c est 1 divisé par le logarithme de base c de b.

log b ( c ) = 1 / log c ( b )

Par exemple:

log 2 (8) = 1 / log 8 (2)

Règle de changement de base du logarithme

Le logarithme de base b de x est le logarithme de base c de x divisé par le logarithme de base c de b.

log b ( x ) = log c ( x ) / log c ( b )

Par exemple, pour calculer le log 2 (8) dans la calculatrice, nous devons changer la base en 10:

log 2 (8) = log 10 (8) / log 10 (2)

Voir: règle de changement de base de journal

Logarithme du nombre négatif

Le logarithme réel de base b de x lorsque x <= 0 n'est pas défini lorsque x est négatif ou égal à zéro:

log b ( x ) n'est pas défini lorsque x ≤ 0

Voir: log du nombre négatif

Logarithme de 0

Le logarithme de base b de zéro n'est pas défini:

log b (0) n'est pas défini

La limite du logarithme de base b de x, lorsque x s'approche de zéro, est moins l'infini:

\ lim_ {x \ to 0 ^ +} \ textup {log} _b (x) = - \ infty

Voir: log de zéro

Logarithme de 1

Le logarithme de base b de un est zéro:

log b (1) = 0

Par exemple, le logarithme en base deux de un est zéro:

log 2 (1) = 0

Voir: log of one

Logarithme de l'infini

La limite du logarithme de base b de x, lorsque x s'approche de l'infini, est égale à l'infini:

lim log b ( x ) = ∞, lorsque x → ∞

Voir: log of infinity

Logarithme de la base

Le logarithme de base b de b est un:

log b ( b ) = 1

Par exemple, le logarithme de base deux de deux est un:

log 2 (2) = 1

Dérivé du logarithme

Quand

f ( x ) = log b ( x )

Alors la dérivée de f (x):

f ' ( x ) = 1 / ( x ln ( b ))

Voir: dérivée log

Intégrale du logarithme

L'intégrale du logarithme de x:

∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C

Par exemple:

∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) - 1 / ln (2) ) + C

Approximation logarithmique

log 2 ( x ) ≈ n + ( x / 2 n - 1),

Logarithme complexe

Pour le nombre complexe z:

z = re iθ = x + iy

Le logarithme complexe sera (n = ...- 2, -1,0,1,2, ...):

Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))

Problèmes de logarithme et réponses

Problème n ° 1

Trouver x pour

log 2 ( x ) + log 2 ( x -3) = 2

Solution:

Utilisation de la règle produit:

log 2 ( x ∙ ( x -3)) = 2

Modification de la forme du logarithme selon la définition du logarithme:

x ∙ ( x -3) = 2 2

Ou

x 2 -3 x -4 = 0

Résolution de l'équation quadratique:

x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1

Puisque le logarithme n'est pas défini pour les nombres négatifs, la réponse est:

x = 4

Problème n ° 2

Trouver x pour

log 3 ( x +2) - log 3 ( x ) = 2

Solution:

En utilisant la règle du quotient:

log 3 (( x +2) / x ) = 2

Modification de la forme du logarithme selon la définition du logarithme:

( x +2) / x = 3 2

Ou

x +2 = 9 x

Ou

8 x = 2

Ou

x = 0,25

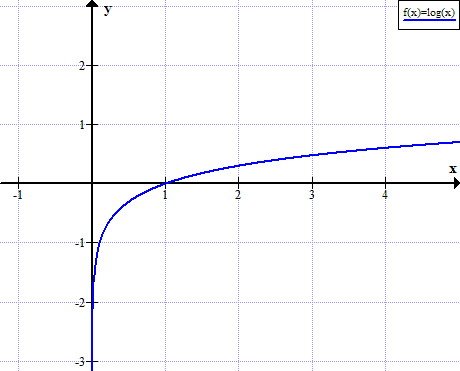
Graphique de log (x)

log (x) n'est pas défini pour les valeurs réelles non positives de x:

Table des logarithmes

x bûche 10 x bûche 2 x log e x
0 indéfini indéfini indéfini
0 + - ∞ - ∞ - ∞
0,0001 -4 -13,287712 -9,210340
0,001 -3 -9,965784 -6.907755
0,01 -2 -6,643856 -4.605170
0,1 -1 -3,321928 -2,302585
1 0 0 0
2 0,301030 1 0,693147
3 0,477121 1,584963 1,098612
4 0,602060 2 1,386294
5 0,698970 2,321928 1,609438
6 0,778151 2,584963 1,791759
7 0,845098 2.807355 1,945910
8 0,903090 3 2,079442
9 0,954243 3,169925 2,197225
10 1 3,321928 2.302585
20 1.301030 4,321928 2.995732
30 1.477121 4,906891 3.401197
40 1,602060 5,321928 3.688879
50 1,698970 5,643856 3.912023
60 1.778151 5,906991 4,094345
70 1,845098 6.129283 4.248495
80 1.903090 6,321928 4,382027
90 1.954243 6,491853 4,499810
100 2 6,643856 4.605170
200 2.301030 7,643856 5,298317
300 2.477121 8.228819 5,703782
400 2.602060 8.643856 5,991465
500 2,698970 8,965784 6,214608
600 2.778151 9.228819 6,396930
700 2,845098 9.451211 6,551080
800 2,903090 9,643856 6,684612
900 2.954243 9,813781 6,802395
1000 3 9,965784 6,907755
10 000 4 13,287712 9.210340

 

Calculateur de logarithme ►

 

Voir également

ALGÈBRE
TABLES RAPIDES