Logarithme naturel - ln (x)
Le logarithme naturel est le logarithme à la base e d'un nombre.
- Définition du logarithme naturel (ln)
- Règles et propriétés du logarithme naturel (LN)
- Logarithme complexe
- Graphique de ln (x)
- Table des logarithmes naturels (ln)
- Calculateur de logarithme naturel
Définition du logarithme naturel
Quand
e y = x
Alors le logarithme de base e de x est
ln ( x ) = log e ( x ) = y
La constante e ou le nombre d'Euler est:
e ≈ 2,71828183
Ln comme fonction inverse de la fonction exponentielle
La fonction logarithmique naturelle ln (x) est la fonction inverse de la fonction exponentielle e x .
Pour x/ 0,
f ( f -1 ( x )) = e ln ( x ) = x
Ou
f -1 ( f ( x )) = ln ( e x ) = x
Règles et propriétés du logarithme naturel
| Nom de la règle | Règle | Exemple |
|---|---|---|
Règle du produit |
ln ( x ∙ y ) = ln ( x ) + ln ( y ) |
ln (3 ∙ 7) = ln (3) + ln (7) |
Règle de quotient |
ln ( x / y ) = ln ( x ) - ln ( y ) |
ln (3 / 7) = ln (3) - ln (7) |
Règle de puissance |
ln ( x y ) = y ∙ ln ( x ) |
ln (2 8 ) = 8 ∙ ln (2) |
En dérivé |
f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x | |
ln intégral |
∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C | |
ln de nombre négatif |
ln ( x ) n'est pas défini lorsque x ≤ 0 | |
ln de zéro |
ln (0) n'est pas défini | |
dans un |
ln (1) = 0 | |
dans l'infini |
lim ln ( x ) = ∞, lorsque x → ∞ | |
| L'identité d'Euler | ln (-1) = i π |
Règle de produit logarithmique
Le logarithme de la multiplication de x et y est la somme du logarithme de x et du logarithme de y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Par exemple:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Règle du quotient logarithmique
Le logarithme de la division de x et y est la différence du logarithme de x et du logarithme de y.
log b ( x / y ) = log b ( x ) - log b ( y )
Par exemple:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Règle de puissance logarithmique
Le logarithme de x élevé à la puissance y est y fois le logarithme de x.
log b ( x y ) = y ∙ log b ( x )
Par exemple:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Dérivée du logarithme naturel
Le dérivé de la fonction logarithmique naturelle est la fonction réciproque.
Quand
f ( x ) = ln ( x )
La dérivée de f (x) est:
f ' ( x ) = 1 / x
Intégrale du logarithme naturel
L'intégrale de la fonction logarithmique naturelle est donnée par:
Quand
f ( x ) = ln ( x )
L'intégrale de f (x) est:
∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C
Ln de 0
Le logarithme naturel de zéro n'est pas défini:
ln (0) n'est pas défini
La limite proche de 0 du logarithme naturel de x, lorsque x s'approche de zéro, est moins l'infini:
![]()
Ln sur 1
Le logarithme naturel de un est zéro:
ln (1) = 0
Ln de l'infini
La limite du logarithme naturel de l'infini, lorsque x s'approche de l'infini est égale à l'infini:
lim ln ( x ) = ∞, lorsque x → ∞
Logarithme complexe
Pour le nombre complexe z:
z = re iθ = x + iy
Le logarithme complexe sera (n = ...- 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
Graphique de ln (x)
ln (x) n'est pas défini pour les valeurs réelles non positives de x:
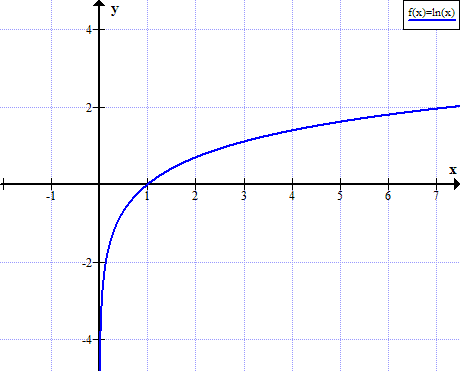
Table des logarithmes naturels
| x | ln x |
|---|---|
| 0 | indéfini |
| 0 + | - ∞ |
| 0,0001 | -9,210340 |
| 0,001 | -6.907755 |
| 0,01 | -4.605170 |
| 0,1 | -2,302585 |
| 1 | 0 |
| 2 | 0,693147 |
| e ≈ 2,7183 | 1 |
| 3 | 1,098612 |
| 4 | 1,386294 |
| 5 | 1,609438 |
| 6 | 1,791759 |
| 7 | 1,945910 |
| 8 | 2,079442 |
| 9 | 2,197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4,094345 |
| 70 | 4.248495 |
| 80 | 4,382027 |
| 90 | 4,499810 |
| 100 | 4.605170 |
| 200 | 5,298317 |
| 300 | 5,703782 |
| 400 | 5,991465 |
| 500 | 6,214608 |
| 600 | 6,396930 |
| 700 | 6,551080 |
| 800 | 6,684612 |
| 900 | 6,802395 |
| 1000 | 6,907755 |
| 10 000 | 9.210340 |
Voir également
- Logarithme (journal)
- Calculateur de logarithme naturel
- Logarithme naturel de zéro
- Logarithme naturel de un
- Logarithme naturel de e
- Logarithme naturel de l'infini
- Logarithme naturel du nombre négatif
- Fonction inverse Ln
- graphe ln (x)
- Table de logarithme naturel
- Calculateur de logarithme
- e constante