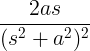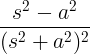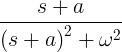Transformation de Laplace

La transformée de Laplace convertit une fonction du domaine temporel en fonction du domaine s par intégration de zéro à l'infini

 de la fonction du domaine temporel, multipliée par e -st .

La transformée de Laplace est utilisée pour trouver rapidement des solutions d'équations différentielles et d'intégrales.

La dérivation dans le domaine temporel est transformée en multiplication par s dans le domaine s.

L'intégration dans le domaine temporel est transformée en division par s dans le domaine s.

Fonction de transformation de Laplace

La transformation de Laplace est définie avec l' opérateur L {}:

F (s) = \ mathcal {L} \ gauche \ {f (t) \ droite \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt

Transformée de Laplace inverse

La transformée de Laplace inverse peut être calculée directement.

Habituellement, la transformée inverse est donnée à partir du tableau des transformations.

Table de transformation de Laplace

Nom de la fonction Fonction du domaine temporel transformation de Laplace

f ( t )

F ( s ) = L { f ( t )}
Constant 1 \ frac {1} {s}
Linéaire t \ frac {1} {s ^ 2}
Puissance

t n

\ frac {n!} {s ^ {n + 1}}
Puissance

t un

Γ ( a +1) ⋅ s - ( a +1)
Exposant

e à

\ frac {1} {sa}
Sinus

pécher à

\ frac {a} {s ^ 2 + a ^ 2}
Cosinus

cos à

\ frac {s} {s ^ 2 + a ^ 2}
Sinus hyperbolique

sinh à

\ frac {a} {s ^ 2-a ^ 2}
Cosinus hyperbolique

cosh à

\ frac {s} {s ^ 2-a ^ 2}
Croissance sinusoïdale

t péché à

\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}
Cosinus croissant

t cos à

\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}
Sinus en décomposition

e -at sin ωt

\ frac {\ omega} {\ gauche (s + a \ droite) ^ 2 + \ omega ^ 2}
Cosinus en décomposition

e -at cos ωt

\ frac {s + a} {\ gauche (s + a \ droite) ^ 2 + \ omega ^ 2}
Fonction Delta

δ ( t )

1

Delta retardé

δ ( ta )

e -as

Propriétés de la transformation de Laplace

Nom de la propriété Fonction du domaine temporel transformation de Laplace Commentaire
 

f ( t )

F ( s )

  
Linéarité af ( t ) + bg ( t ) aF ( s ) + bG ( s ) a , b sont constants
Changement d'échelle f ( at ) \ frac {1} {a} F \ gauche (\ frac {s} {a} \ droite) a / 0
Décalage e -at f ( t ) F ( s + a )  
Retard f ( ta ) e - comme F ( s )  
Dérivation \ frac {df (t)} {dt} sF ( s ) - f (0)  
N-ième dérivation \ frac {d ^ nf (t)} {dt ^ n} s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0)  
Puissance t n f ( t ) (-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}  
L'intégration \ int_ {0} ^ {t} f (x) dx \ frac {1} {s} F (s)  
Réciproque \ frac {1} {t} f (t) \ int_ {s} ^ {\ infty} F (x) dx  
Convolution f ( t ) * g ( t ) F ( s ) ⋅ G ( s ) * est l'opérateur de convolution
Fonction périodique f ( t ) = f ( t + T ) \ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx  

Exemples de transformation de Laplace

Exemple 1

Trouvez la transformée de f (t):

f ( t ) = 3 t + 2 t 2

Solution:

ℒ { t } = 1 / s 2

ℒ { t 2 } = 2 / s 3

F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3

 

Exemple # 2

Trouvez la transformée inverse de F (s):

F ( s ) = 3 / ( s 2 + s - 6)

Solution:

Afin de trouver la transformée inverse, nous devons changer la fonction de domaine s en une forme plus simple:

F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)

[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]

a ( s +3) + b ( s -2) = 3

Pour trouver a et b, nous obtenons 2 équations - l'un des coefficients s et la seconde des autres:

( a + b ) s + 3 a -2 b = 3

a + b = 0, 3 a -2 b = 3

a = 3/5, b = -3/5

F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)

Maintenant F (s) peut être transformé facilement en utilisant le tableau des transformations pour la fonction exposant:

f ( t ) = (3/5) e 2 t - (3/5) e -3 t

 

Voir également

CALCUL
TABLES RAPIDES