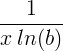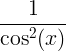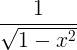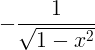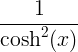כללי נגזרת

כללים וחוקים נגזרים. נגזרת של טבלת הפונקציות.

הגדרה נגזרת
כללי נגזרת
נגזרת של טבלת הפונקציות
דוגמאות נגזרות

הגדרה נגזרת

הנגזרת של פונקציה היא היחס בין ההבדל בין ערך הפונקציה f (x) בנקודות x + Δx ו- x עם Δx, כאשר Δx קטן לאין ערוך. הנגזרת היא שיפוע או שיפוע הפונקציה של קו המשיק בנקודה x.

$f '(x) = \ lim _ {\ Delta x \ to 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}$

נגזרת שנייה

הנגזרת השנייה ניתנת על ידי:

או פשוט לגזור את הנגזרת הראשונה:

נגזרת N

N th נגזר מחושב על ידי גזירת f (x) n פעמים.

N th נגזרת שווה לנגזרת של (n-1) נגזרת:

f ^{( n )} ( x ) = [ f ^{( n -1)} ( x )] '

דוגמא:

מצא את הנגזרת הרביעית של

f ( x ) = 2 x ⁵

f ⁽⁴⁾ ( x ) = [2 x ⁵ ] '' '' = [10 x ⁴ ] '' '= [40 x ³ ]' '= [120 x ² ]' = 240 x

נגזרת בגרף הפונקציה

הנגזרת של פונקציה היא שיפוע הקו המשיק.

כללי נגזרת

כלל סכום נגזר	( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
כלל מוצר נגזר	( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
כלל המנה הנגזרת	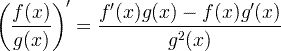$\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( איקס)}$
כלל שרשרת נגזרת	f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

כלל סכום נגזר

כאשר a ו- b הם קבועים.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

דוגמא:

מצא את הנגזרת של:

3 x ² + 4 x.

על פי כלל הסכום:

a = 3, b = 4

f ( x ) = x ² , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x ² + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

כלל מוצר נגזר

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

כלל המנה הנגזרת

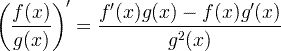
$\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( איקס)}$

כלל שרשרת נגזרת

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

ניתן להבין טוב יותר את הכלל הזה באמצעות הסימון של לגראנז ':

$\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}$

קירוב לינארי של פונקציה

עבור Δx קטן, אנו יכולים לקבל קירוב ל- f (x ₀ + Δx), כאשר אנו יודעים f (x ₀ ) ו- f '(x ₀ ):

f ( x ₀ + Δ x ) ≈ f ( x ₀ ) + f '( x ₀ ) ⋅Δ x

נגזרת של טבלת הפונקציות

שם פונקציה	פוּנקצִיָה	נגזר
שם פונקציה	f ( x )	f '( x )
קָבוּעַ	קונסט	0
לינארי	x	1
כּוֹחַ	x ^א	גרזן ^a-¹
אקספוננציאלי	e ^x	e ^x
אקספוננציאלי	א ^x	a ^x ln a
לוגריתם טבעי	ln ( x )
לוֹגָרִיתְם	יומן _ב ( x )
סינוס	חטא x	cos x
קוסינוס	cos x	-סין x
מַשִׁיק	שזוף x
ארקסין	קשת x
ארקוזין	ארקוס x
ארקטנג'נט	ארקטאן x
סינוס היפרבולי	sinh x	cosh x
קוסינוס היפרבולי	cosh x	sinh x
משיק היפרבולי	tanh x
סינוס היפרבולי הפוך	sinh ^-1 x
קוסינוס היפרבולי הפוך	cosh ^-1 x
משיק היפרבולי הפוך	tanh ^-1 x