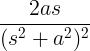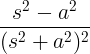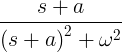טרנספורמציה Laplace

טרנספורמציה של Laplace ממירה פונקציה של תחום זמן לפונקציה של s-domain על ידי שילוב מאפס לאינסוף

של פונקציית תחום הזמן, כפול e ^-st .

התמורה Laplace משמשת למציאת פתרונות במהירות למשוואות דיפרנציאליות ואינטגרלים.

נגזרת בתחום הזמן הופכת לכפל ב- s בתחום ה- s.

שילוב בתחום הזמן הופך לחלוקה על ידי s בתחום ה- s.

פונקצית שינוי Laplace

הטרנספורמציה של Laplace מוגדרת באמצעות האופרטור L {}:

$F (s) = \ mathcal {L} \ left \ {f (t) \ right \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

ניתן לחשב את טרנספורמציית Laplace ההפוכה ישירות.

בדרך כלל הטרנספורמציה ההפוכה ניתנת מטבלת הטרנספורמציות.

שם פונקציה	פונקציית תחום זמן	Laplace טרנספורמציה
שם פונקציה	f ( t )	F ( s ) = L { f ( t )}
קָבוּעַ	1	$\ frac {1} {s}$
לינארי	t	$\ frac {1} {s ^ 2}$
כּוֹחַ	t ⁿ	$\ frac {n!} {s ^ {n + 1}}$
כּוֹחַ	t ^a	Γ ( a +1) ⋅ s ^{- ( a +1)}
מַעֲרִיך	ה ^ב	$\ frac {1} {sa}$
סינוס	לחטוא ב	$\ frac {a} {s ^ 2 + a ^ 2}$
קוסינוס	cos ב	$\ frac {s} {s ^ 2 + a ^ 2}$
סינוס היפרבולי	חטא ב	$\ frac {a} {s ^ 2-a ^ 2}$
קוסינוס היפרבולי	קוסם ב	$\ frac {s} {s ^ 2-a ^ 2}$
גידול סינוס	לא לחטוא ב	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
גידול קוסינוס	t cos at	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
ריקבון סינוס	דואר ^בטיילת חטא ωt	$\ frac {\ omega} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
קוסינוס מתפורר	דואר ^בטיילת cos ωt	$\ frac {s + a} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
פונקציית דלתא	δ ( t )	1
דלתא מושהית	δ ( ta )	e ^-as

שם הנכס	פונקציית תחום זמן	Laplace טרנספורמציה	תגובה
	f ( t )	F ( ים )
לינאריות	af ( t ) + bg ( t )	AF ( s ) + BG ( s )	a , b קבועים
שינוי קנה מידה	f ( ב )	$\ frac {1} {a} F \ left (\ frac {s} {a} \ right)$	a / 0
מִשׁמֶרֶת	e ^-at f ( t )	F ( s + a )
לְעַכֵּב	f ( ta )	e ^{- כמו} F ( s )
גִזרָה	$\ frac {df (t)} {dt}$	sF ( s ) - f (0)
נגזרת N	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
כּוֹחַ	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
שילוב	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F (ים)$
הֲדָדִי	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
קונבולוציה	f ( t ) * g ( t )	F ( s ) ⋅ G ( s )	* הוא מפעיל הפיתול
תפקוד תקופתי	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$