होम / गणित / संभावना /विचलन

झगड़ा

प्रायिकता और सांख्यिकी में, एक यादृच्छिक चर का संस्करण औसत मान से वर्ग दूरी का औसत मूल्य है। यह दर्शाता है कि यादृच्छिक चर को माध्य मान के पास कैसे वितरित किया जाता है। लघु विचरण इंगित करता है कि यादृच्छिक चर को माध्य मान के पास वितरित किया जाता है। बिग विचरण इंगित करता है कि यादृच्छिक चर को माध्य मान से दूर वितरित किया गया है। उदाहरण के लिए, सामान्य वितरण के साथ, संकीर्ण घंटी वक्र में छोटा विचरण होगा और चौड़ी घंटी वक्र में बड़ा विचरण होगा।

विरेचन परिभाषा;

यादृच्छिक चर X का प्रसरण X के अंतर के वर्गों का अपेक्षित मान और अपेक्षित मान μ है।

σ ² = वार ( एक्स ) = ई [( एक्स - μ ) ² ]

विचरण की परिभाषा से हम प्राप्त कर सकते हैं

σ ² = वार ( एक्स ) = ई ( एक्स ² ) - μ ²

निरंतर यादृच्छिक चर की भिन्नता

माध्य मान μ और प्रायिकता घनत्व फ़ंक्शन f (x) के साथ निरंतर यादृच्छिक चर के लिए:

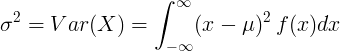
$\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx$

या

$Var (X) = \ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2$

असतत यादृच्छिक चर की भिन्नता

असतत रैंडम वेरिएबल X के लिए माध्य मान μ और प्रायिकता मास फंक्शन P (x):

$\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)$

या

$Var (X) = \ बाएँ [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2$

विचरण के गुण

जब X और Y स्वतंत्र यादृच्छिक चर होते हैं:

वार ( X + Y ) = वार ( X ) + वार ( Y )

मानक विचलन ►

यह सभी देखें

संभावना और सांख्यिकी

रैपिड टाइलें