Variancia

A valószínűségben és a statisztikában a véletlen változó szórása a négyzet átlagos távolságának átlagos értéke. Azt ábrázolja, hogy a véletlen változó hogyan oszlik el az átlagérték közelében. Kis eltérés azt jelzi, hogy a véletlen változó eloszlik az átlagérték közelében. A nagy variancia azt jelzi, hogy a véletlen változó az átlagértéktől messze oszlik el. Például normál eloszlás esetén a keskeny haranggörbének kis, a széles haranggörbének pedig nagy a szórása.

Varianciadefiníció

Az X véletlen változó varianciája az X különbség négyzetének várható értéke és a várható μ értéke.

σ 2 = Var ( X ) = E [( X - μ ) 2 ]

A variancia meghatározásából kaphatunk

σ 2 = Var ( X ) = E ( X 2 ) - μ 2

Folyamatos véletlen változó varianciája

Folyamatos véletlen változó esetén μ átlagos érték és az f (x) valószínűségi sűrűség függvény:

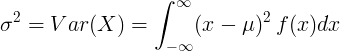
\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx

vagy

Var (X) = \ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2

Diszkrét véletlen változó varianciája

Diszkrét X véletlen változó esetén μ átlagos érték és P (x) valószínűségi tömegfüggvény:

\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)

vagy

Var (X) = \ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2

A variancia tulajdonságai

Ha X és Y független véletlen változó:

Var ( X + Y ) = Var ( X ) + Var ( Y )

 

Szórás ►

 

Lásd még

VALÓSZÍNŰSÉG ÉS STATISZTIKA
GYORS TÁBLÁZATOK