Valószínűségi eloszlás

A valószínűség és a statisztika szerint az eloszlás egy véletlen változó jellemzője, leírja a véletlen változó valószínűségét az egyes értékekben.

Minden eloszlásnak van egy bizonyos valószínűségi sűrűségi és valószínűségi eloszlásfüggvénye.

Noha határozatlan számú valószínűségi eloszlás létezik, több közös eloszlás van használatban.

A valószínűségi eloszlást az F (x) kumulatív eloszlásfüggvény írja le,

amely annak valószínűsége, hogy az X véletlen változó x-nél kisebb vagy egyenlő értéket kap:

F ( x ) = P ( X ≤ x )

Az F (x) kumulatív eloszlásfüggvényt az X véletlenszerű változó f (u) valószínűségi sűrűségfüggvényének integrálásával számoljuk ki.

Az F (x) kumulatív eloszlásfüggvény kiszámítása az X diszkrét véletlen változó P (u) valószínűségi tömegfüggvényének összegzésével történik.

A folyamatos eloszlás a folytonos véletlenszerű változó eloszlása.

...

Forgalmazás neve	Terjesztési szimbólum	Valószínűségi sűrűségfüggvény (pdf)	Átlagos	Variancia
		f _X ( x )	μ = E ( X )	σ ² = Var ( X )
Normál / gaussian	X ~ N (μ, σ ² )	$\ frac {1} {\ sigma \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}}$	μ	σ ²
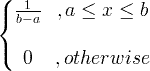Egyenruha	X ~ U ( a , b )	$\ begin {Bmatrix} \ frac {1} {ba} &, a \ leq x \ leq b \\ & \\ 0 &, különben \ end {mátrix}$		$\ frac {(ba) ^ 2} {12}$
Exponenciális	X ~ exp (λ)	$\ begin {Bmatrix} \ lambda e ^ {- \ lambda x} & x \ geq 0 \\ 0 & x <0 \ end {mátrix}$	$\ frac {1} {\ lambda}$	$\ frac {1} {\ lambda ^ 2}$
Gamma	X ~ gamma ( c , λ)	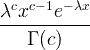$\ frac {\ lambda ^ cx ^ {c-1} e ^ {- \ lambda x}} {\ Gamma (c)}$ x / 0, c / 0, λ/ 0	$\ frac {c} {\ lambda}$	$\ frac {c} {\ lambda ^ 2}$
Chi tér	X ~ χ ² ( k )	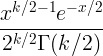$\ frac {x ^ {k / 2-1} e ^ {- x / 2}} {2 ^ {k / 2} \ Gamma (k / 2)}$	k	2 k
Wishart
F	X ~ F ( k ₁, k ₂ )
Beta
Weibull
Napló-normális	X ~ LN (μ, σ ² )
Rayleigh
Cauchy
Dirichlet
Laplace
Levy
Rizs
Diák t

A diszkrét eloszlás egy diszkrét véletlen változó eloszlása.

...

Forgalmazás neve	Terjesztési szimbólum	Valószínűség tömegfüggvény (pmf)		Átlagos	Variancia
		f _x ( k ) = P ( X = k ) k = 0,1,2, ...		E ( x )	Var ( x )
Binomial	X ~ Bin ( n , p )	$\ binom {n} {k} p ^ {k} (1-p) ^ {nk}$		np	np (1- p )
Poisson	X ~ Poisson (λ)		λ ≥ 0	λ	λ
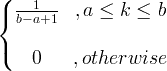Egyenruha	X ~ U ( a, b )	$\ begin {Bmatrix} \ frac {1} {b-a + 1} &, a \ leq k \ leq b \\ & \\ 0 &, különben \ end {matrix}$		$\ frac {a + b} {2}$	$\ frac {(b-a + 1) ^ {2} -1} {12}$
Geometriai	X ~ Geom ( p )	$p (1-p) ^ {k}$		$\ frac {1-p} {p}$	$\ frac {1-p} {p ^ 2}$
Hipergeometrikus	X ~ HG ( N , K , n )		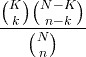N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N	$\ frac {nK} {N}$	$\ frac {nK (NK) (Nn)} {N ^ 2 (N-1)}$
Bernoulli	X ~ Bern ( p )	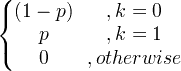$\ begin {Bmatrix} (1-p) &, k = 0 \\ p &, k = 1 \\ 0 &, különben \ end {mátrix}$		p	p (1- p )

Lásd még