Convoluzione
La convoluzione è la funzione di correlazione di f (τ) con la funzione inversa g (t-τ).
L'operatore di convoluzione è il simbolo dell'asterisco * .
- Convoluzione continua
- Convoluzione discreta
- Convoluzione discreta 2D
- Filtra l'implementazione con la convoluzione
- Teorema di convoluzione
Convoluzione continua
La convoluzione di f (t) eg (t) è uguale all'integrale di f (τ) per f (t-τ):
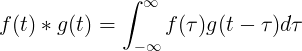
Convoluzione discreta
La convoluzione di 2 funzioni discrete è definita come:
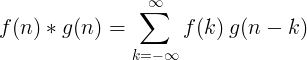
Convoluzione discreta 2D
La convoluzione discreta bidimensionale viene solitamente utilizzata per l'elaborazione delle immagini.
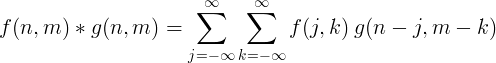
Filtra l'implementazione con la convoluzione
Possiamo filtrare il segnale di ingresso discreto x (n) per convoluzione con la risposta all'impulso h (n) per ottenere il segnale di uscita y (n).
y ( n ) = x ( n ) * h ( n )
Teorema di convoluzione
La trasformata di Fourier di una moltiplicazione di 2 funzioni è uguale alla convoluzione delle trasformate di Fourier di ciascuna funzione:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
La trasformata di Fourier di una convoluzione di 2 funzioni è uguale alla moltiplicazione delle trasformate di Fourier di ciascuna funzione:
ℱ { f * g } = ℱ { f } ⋅ ℱ { g }
Teorema di convoluzione per trasformata di Fourier continua
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
Teorema di convoluzione per trasformata discreta di Fourier
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
Teorema di convoluzione per trasformata di Laplace
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )
Guarda anche
CALCOLO
- Limite
- Derivato
- Integrante
- Serie
- Trasformata di Laplace
- Convoluzione
- Simboli di calcolo
TAVOLI RAPIDI