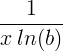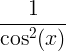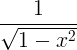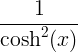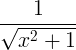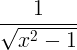Regole derivate

Regole e leggi derivate. Tabella delle derivate delle funzioni.

Definizione derivata

La derivata di una funzione è il rapporto della differenza del valore della funzione f (x) nei punti x + Δx e x con Δx, quando Δx è infinitesimamente piccolo. La derivata è la funzione pendenza o pendenza della retta tangente nel punto x.

 

f '(x) = \ lim _ {\ Delta x \ to 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}

Seconda derivata

La derivata seconda è data da:

O semplicemente derivare la prima derivata:

f '' (x) = (f '(x))'

Ennesima derivata

La derivata n- esima viene calcolata derivando f (x) n volte.

La derivata n- esima è uguale alla derivata della derivata (n-1):

f ( n ) ( x ) = [ f ( n -1) ( x )] '

Esempio:

Trova la quarta derivata di

f ( x ) = 2 x 5

f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x

Derivata su grafico di funzione

La derivata di una funzione è la pendenza della retta tangenziale.

Regole derivate

Regola della somma derivativa

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Regola del prodotto derivato

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Regola del quoziente derivato 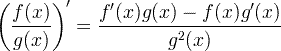\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( X)}
Regola della catena derivativa

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Regola della somma derivativa

Quando un e b sono costanti.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Esempio:

Trova la derivata di:

3 x 2 + 4 x.

Secondo la regola della somma:

a = 3, b = 4

f ( x ) = x 2 , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Regola del prodotto derivato

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Regola del quoziente derivato

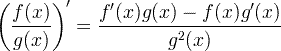
\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( X)}

Regola della catena derivativa

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Questa regola può essere meglio compresa con la notazione di Lagrange:

\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}

Approssimazione lineare della funzione

Per Δx piccolo, possiamo ottenere un'approssimazione af (x 0 + Δx), quando sappiamo f (x 0 ) e f '(x 0 ):

f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x

Tabella delle derivate delle funzioni

Nome della funzione Funzione Derivato

f ( x )

 f '( x )
Costante

const

0

Lineare

x

1

Energia

x a

ascia a- 1
Esponenziale

e x

e x
Esponenziale

una x

a x ln a
Logaritmo naturale

ln ( x )

Logaritmo

log b ( x )

Sine

peccato x

cos x
Coseno

cos x

-sin x
Tangente

tan x

Arcoseno

arcsin x

Arccosine

arccos x

Arcotangente

arctan x
Seno iperbolico

sinh x

cosh x
Coseno iperbolico

cosh x

sinh x
Tangente iperbolica

tanh x

Seno iperbolico inverso

sinh -1 x

Coseno iperbolico inverso

cosh -1 x

Tangente iperbolica inversa

tanh -1 x

Esempi derivati

Esempio 1

f ( x ) = x 3 +5 x 2 + x +8

f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1

Esempio n. 2

f ( x ) = sin (3 x 2 )

Quando si applica la regola della catena:

f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x

Seconda prova della derivata

Quando la prima derivata di una funzione è zero nel punto x 0 .

f '( x 0 ) = 0

Quindi la derivata seconda al punto x 0 , f '' (x 0 ), può indicare il tipo di quel punto:

 

f '' ( x 0 )/ 0

 minimo locale

f '' ( x 0 ) <0

 massimo locale

f '' ( x 0 ) = 0

 indeterminato

 

Guarda anche

CALCOLO
TAVOLI RAPIDI