완전한

적분은 파생의 역 동작입니다.

함수의 적분은 함수의 그래프 아래 영역입니다.

무한 적분 정의

언제 dF (x) / dx = f (x) =/ 적분 (f (x) * dx) = F (x) + c

무한 정수 속성

적분 (f (x) + g (x)) * dx = 적분 (f (x) * dx) + 적분 (g (x) * dx)

적분 (a * f (x) * dx) = a * integral (f (x) * dx)

적분 (f (a * x) * dx) = 1 / a * F (a * x) + c

적분 (f (x + b) * dx) = F (x + b) + c

적분 (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

적분 (df (x) / dx * dx) = f (x)

적분 변수 변경

언제 x = g (t)  과 dx = g '(t) * dt

적분 (f (x) * dx) = 적분 (f (g (t)) * g '(t) * dt)

부품 별 통합

적분 (f (x) * g '(x) * dx) = f (x) * g (x)-적분 (f'(x) * g (x) * dx)

적분 테이블

적분 (f (x) * dx = F (x) + c

적분 (a * dx) = a * x + c

적분 (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, a </-1 일 때

적분 (1 / x * dx) = ln (abs (x)) + c

적분 (e ^ x * dx) = e ^ x + c

적분 (a ^ x * dx) = a ^ x / ln (x) + c

적분 (ln (x) * dx) = x * ln (x)-x + c

적분 (sin (x) * dx) = -cos (x) + c

적분 (cos (x) * dx) = sin (x) + c

적분 (tan (x) * dx) = -ln (abs (cos (x))) + c

적분 (arcsin (x) * dx) = x * arcsin (x) + sqrt (1-x ^ 2) + c

적분 (arccos (x) * dx) = x * arccos (x)-sqrt (1-x ^ 2) + c

적분 (arctan (x) * dx) = x * arctan (x)-1 / 2 * ln (1 + x ^ 2) + c

적분 (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

적분 (1 / sqrt (a ^ 2-x ^ 2) * dx) = arcsin (x / a) + c

적분 (1 / sqrt (x ^ 2 +-a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 +-a ^ 2)) + c

적분 (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

적분 (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * arctan (x / a) + c

적분 (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

적분 (sinh (x) * dx) = cosh (x) + c

적분 (cosh (x) * dx) = sinh (x) + c

적분 (tanh (x) * dx) = ln (cosh (x)) + c

 

명확한 통합 정의

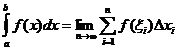
적분 (a..b, f (x) * dx) = lim (n-/ inf, sum (i = 1..n, f (z (i)) * dx (i)))  

언제 x0 = a, xn = b

dx (k) = x (k)-x (k-1)

x (k-1) <= z (k) <= x (k)

명확한 적분 계산

언제  ,

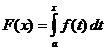  dF (x) / dx = f (x)  과

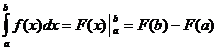
적분 (a..b, f (x) * dx) = F (b)-F (a)  

명확한 정수 속성

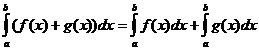
적분 (a..b, (f (x) + g (x)) * dx) = 적분 (a..b, f (x) * dx) + 적분 (a..b, g (x) * dx )

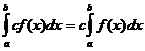
적분 (a..b, c * f (x) * dx) = c * integral (a..b, f (x) * dx)

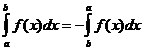
적분 (a..b, f (x) * dx) =-적분 (b..a, f (x) * dx)

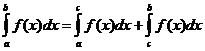
적분 (a..b, f (x) * dx) = 적분 (a..c, f (x) * dx) + 적분 (c..b, f (x) * dx)

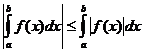
abs (적분 (a..b, f (x) * dx)) <= 적분 (a..b, abs (f (x)) * dx)

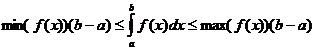min (f (x)) * (ba) <= 적분 (a..b, f (x) * dx) <= max (f (x)) * (ba)  언제 x 구성원 [a, b]

적분 변수 변경

언제 x = g (t)  , dx = g '(t) * dt  , g (알파) = a  , g (베타) = b

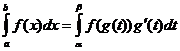
적분 (a..b, f (x) * dx) = 적분 (alpha..beta, f (g (t)) * g '(t) * dt)

부품 별 통합

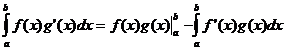
적분 (a..b, f (x) * g '(x) * dx) = 적분 (a..b, f (x) * g (x) * dx)-적분 (a..b, f' (x) * g (x) * dx)

평균값 정리

하면 F ( x는 ) 연속 포인트가 c는 [a, b]의 구성원입니다.  그래서

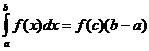
적분 (a..b, f (x) * dx) = f (c) * (ba)   

정규 적분의 사다리꼴 근사

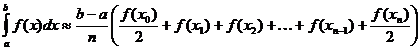
적분 (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

감마 함수

감마 (x) = 적분 (0..inf, t ^ (x-1) * e ^ (-t) * dt

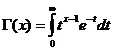
감마 함수는 x/ 0에 대해 수렴합니다 .

감마 함수 속성

G ( x +1) = x G ( x )

G ( n +1) = n ! , 때 N ℕ (양의 정수). 의 회원이다

베타 기능

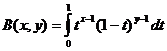
B (x, y) = 적분 (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

베타 기능과 감마 기능 관계

B (x, y) = 감마 (x) * 감마 (y) / 감마 (x + y)

 

 

 

계산법
빠른 테이블