Konvoliucija
Konvoliucija yra f (τ) koreliacijos funkcija su atvirkštine funkcija g (t-τ).
Konvoliucijos operatorius yra žvaigždutės simbolis * .
- Nuolatinė konvoliucija
- Diskretioji konvekcija
- 2D diskretioji konvekcija
- Filtruoti įgyvendinimą su konvekcija
- Konvoliucijos teorema
Nuolatinė konvoliucija
F (t) ir g (t) konvekcija yra lygi f (τ) kartų f (t-τ) integralui:
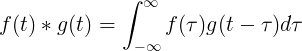
Diskretioji konvekcija
2 atskirų funkcijų konvoliucija apibrėžiama taip:
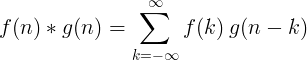
2D diskretioji konvekcija
Vaizdų apdorojimui paprastai naudojama 2 matmenų diskretioji konvekcija.
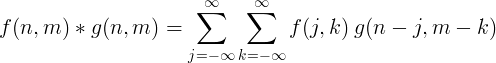
Filtruoti įgyvendinimą su konvekcija
Diskretų įvesties signalą x (n) galime filtruoti konvoliucijos būdu su impulsiniu atsaku h (n), kad gautume išėjimo signalą y (n).
y ( n ) = x ( n ) * h ( n )
Konvoliucijos teorema
2 funkcijų padauginimo Furjė transformacija yra lygi kiekvienos funkcijos Furjė transformacijų konvoliucijai:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
2 funkcijų konvekcijos Furjė transformacija yra lygi kiekvienos funkcijos Furjė transformacijų dauginimui:
ℱ { f * g } = ℱ { f } ⋅ ℱ { g }
Nuolatinės Furjė transformacijos konvoliucijos teorema
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
Diskrečios Furjė transformacijos konvoliucijos teorema
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
Laplaso transformacijos konvoliucijos teorema
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )
Taip pat žiūrėkite
KALKULAS
- Apriboti
- Išvestinė
- Integralus
- Serija
- Laplaso transformacija
- Konvoliucija
- Skaičiavimo simboliai
GREITOS LENTELĖS