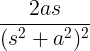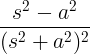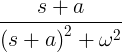Laplaso transformacija
- Laplaso transformacijos funkcija
- Laplaso transformacinė lentelė
- Laplaso transformacijos savybės
- Laplaso transformacijos pavyzdžiai
Laplaso transformacija laiko domeno funkciją paverčia s srities funkcija integruojant nuo nulio iki begalybės
laiko domeno funkcijos, padaugintos iš e -st .
Laplaso transformacija naudojama norint greitai rasti diferencialinių lygčių ir integralų sprendimus.
Laiko domeno išvedimas paverčiamas dauginimu iš s s srityje.
Integracija laiko srityje transformuojama į dalijimą s s srityje.
Laplaso transformacijos funkcija
Laplaso transformacija apibrėžiama naudojant operatorių L {}:
![]()
Atvirkštinė Laplaso transformacija
Atvirkštinę Laplaso transformaciją galima apskaičiuoti tiesiogiai.
Paprastai atvirkštinė transformacija pateikiama iš transformacijų lentelės.
Laplaso transformacinė lentelė
| Funkcijos pavadinimas | Laiko domeno funkcija | Laplaso transformacija |
|---|---|---|
f ( t ) |
F ( s ) = L { f ( t )} |
|
| Nuolatinis | 1 | |
| Linijinis | t | |
| Galia | t n |
|
| Galia | t a |
Γ ( 1) ⋅ S - ( 1) |
| Eksponentas | e ne |
|
| Sinusas | nuodėmė ne |
|
| Kosinusas | cos ne |
|
| Hiperbolinis sinusas | sinh at |
|
| Hiperbolinis kosinusas | ch ne |
|
| Augantis sinusas | T nuodėmė ne |
|
| Augantis kosinusas | t cos at |
|
| Gendantis sinusas | e -at sin ωt |
|
| Gendantis kosinusas | e -at cos ωt |
|
| Delta funkcija | δ ( t ) |
1 |
| Delta delta | δ ( ta ) |
e -as |
Laplaso transformacijos savybės
| Nuosavybės pavadinimas | Laiko domeno funkcija | Laplaso transformacija | Pakomentuokite |
|---|---|---|---|
f ( t ) |
F ( s ) |
||
| Linijiškumas | af ( t ) + bg ( t ) | aF ( s ) + bG ( s ) | a , b yra pastovūs |
| Mastelio keitimas | f ( at ) | |
a / 0 |
| „Shift“ | e -at f ( t ) | F ( s + a ) | |
| Delsimas | f ( ta ) | e - kaip F ( s ) | |
| Išvedimas | |
sF ( s ) - f (0) | |
| N-tasis darinys | |
s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0) | |
| Galia | t n f ( t ) | |
|
| Integracija | |
|
|
| Abipusis | |
|
|
| Konvoliucija | f ( t ) * g ( t ) | F ( s ) ⋅ G ( s ) | * yra konvoliucijos operatorius |
| Periodinė funkcija | f ( t ) = f ( t + T ) | |
Laplaso transformacijos pavyzdžiai
1 pavyzdys
Raskite f (t) transformaciją:
f ( t ) = 3 t + 2 t 2
Sprendimas:
ℒ { t } = 1 / s 2
ℒ { t 2 } = 2 / s 3
F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3
2 pavyzdys
Raskite atvirkštinę F (s) transformaciją:
F ( s ) = 3 / ( s 2 + s - 6)
Sprendimas:
Norėdami rasti atvirkštinę transformaciją, turime pakeisti s srities funkciją į paprastesnę formą:
F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)
[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]
a ( s +3) + b ( s -2) = 3
Norėdami rasti a ir b, gausime 2 lygtis - vieną iš s koeficientų ir antrą iš likusių:
( a + b ) s + 3 a -2 b = 3
a + b = 0, 3 a -2 b = 3
a = 3/5, b = -3/5
F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)
Dabar F (s) gali būti lengvai transformuojami, naudojant eksponento funkcijos transformacijų lentelę:
f ( t ) = (3/5) e 2 t - (3/5) e -3 t
Taip pat žiūrėkite
KALKULAS
- Apriboti
- Išvestinė
- Integralus
- Serija
- Laplaso transformacija
- Konvoliucija
- Skaičiavimo simboliai
GREITOS LENTELĖS