Konversija
Konversija ir f (τ) korelācijas funkcija ar apgriezto funkciju g (t-τ).
Konversijas operators ir zvaigznītes simbols * .
- Nepārtraukta konvekcija
- Diskrēta konvekcija
- 2D diskrētā konvekcija
- Filtrēt ieviešanu ar konvekciju
- Konversijas teorēma
Nepārtraukta konvekcija
F (t) un g (t) konvekcija ir vienāda ar f (τ) un f (t-τ) reizinājumu:
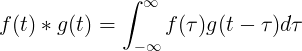
Diskrēta konvekcija
2 diskrēto funkciju konversija ir definēta kā:
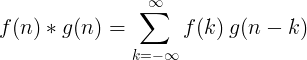
2D diskrētā konvekcija
Attēlu apstrādei parasti tiek izmantota 2 dimensiju diskrēta konvekcija.
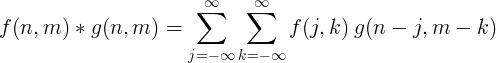
Filtrēt ieviešanu ar konvekciju
Diskrēto ieejas signālu x (n) mēs varam filtrēt, konvolējot ar impulsa reakciju h (n), lai iegūtu izejas signālu y (n).
y ( n ) = x ( n ) * h ( n )
Konversijas teorēma
2 funkciju reizināšanas Furjē transformācija ir vienāda ar katras funkcijas Furjē transformāciju konvekciju:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
2 funkciju konvolūcijas Furjē transformācija ir vienāda ar katras funkcijas Furjē transformāciju reizinājumu:
ℱ { f * g } = ℱ { f } ⋅ ℱ { g }
Konversijas teorēma nepārtrauktai Furjē transformācijai
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
Konversijas teorēma diskrētai Furjē transformācijai
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
Konversijas teorēma Laplasa transformācijai
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )
Skatīt arī
KALKULS
- Ierobežot
- Atvasinājums
- Neatņemama
- Sērija
- Laplasa transformācija
- Konversija
- Rēķina simboli
ĀTRAS TABULAS