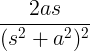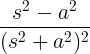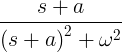Laplasa pārveidošana
- Laplasa transformācijas funkcija
- Laplasa transformācijas galds
- Laplasa transformācijas īpašības
- Laplasa transformācijas piemēri
Laplasa transformācija laika domēna funkciju pārveido par s-domēna funkciju, integrējot no nulles līdz bezgalībai
laika domēna funkcijas, kas reizināta ar e -st .
Laplasa transformāciju izmanto, lai ātri atrastu risinājumus diferenciālvienādojumiem un integrāļiem.
Atvasinājums laika domēnā tiek pārveidots par reizinājumu ar s s domēnā.
Laika domēna integrācija tiek pārveidota par dalīšanu ar s domēnā s.
Laplasa transformācijas funkcija
Laplasa transformācija tiek definēta ar operatoru L {}:
![]()
Apgrieztā Laplasa pārveidošana
Apgriezto Laplasa transformāciju var aprēķināt tieši.
Parasti apgrieztā transformācija tiek dota no transformāciju tabulas.
Laplasa transformācijas galds
| Funkcijas nosaukums | Laika domēna funkcija | Laplasa transformācija |
|---|---|---|
f ( t ) |
F ( s ) = L { f ( t )} |
|
| Pastāvīgs | 1 | |
| Lineāra | t | |
| Jauda | t n |
|
| Jauda | t a |
Γ ( +1) ⋅ s - ( +1) |
| Eksponents | e plkst |
|
| Sine | grēks at |
|
| Kosinuss | cos plkst |
|
| Hiperboliska sinusa | sinh pie |
|
| Hiperboliskais kosinuss | cosh plkst |
|
| Aug sinusa | t grēks at |
|
| Pieaugošais kosinuss | t cos plkst |
|
| Pūstoša sinusa | e -at grēks ωt |
|
| Pūstošs kosinuss | e -at cos ωt |
|
| Delta funkcija | δ ( t ) |
1 |
| Aizkavēta delta | δ ( ta ) |
e- kā |
Laplasa transformācijas īpašības
| Īpašuma nosaukums | Laika domēna funkcija | Laplasa transformācija | Komentēt |
|---|---|---|---|
f ( t ) |
F ( s ) |
||
| Linearitāte | af ( t ) + bg ( t ) | aF ( s ) + bG ( s ) | a , b ir nemainīgi |
| Mēroga maiņa | f ( pie ) | |
a / 0 |
| Shift | e -at f ( t ) | F ( s + a ) | |
| Kavēšanās | f ( ta ) | e - kā F ( s ) | |
| Atvasinājums | |
sF ( s ) - f (0) | |
| N-tas atvasinājums | |
s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0) | |
| Jauda | t n f ( t ) | |
|
| Integrācija | |
|
|
| Abpusējs | |
|
|
| Konversija | f ( t ) * g ( t ) | F ( s ) ⋅ G ( s ) | * ir konvolūcijas operators |
| Periodiska funkcija | f ( t ) = f ( t + T ) | |
Laplasa transformācijas piemēri
1. piemērs
Atrodiet f (t) pārveidojumu:
f ( t ) = 3 t + 2 t 2
Risinājums:
ℒ { t } = 1 / s 2
ℒ { t 2 } = 2 / s 3
F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3
2. piemērs
Atrodiet F (s) apgriezto transformāciju:
F ( s ) = 3 / ( s 2 + s - 6)
Risinājums:
Lai atrastu apgriezto transformāciju, mums s domēna funkcija jāmaina uz vienkāršāku formu:
F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)
[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]
a ( s +3) + b ( s -2) = 3
Lai atrastu a un b, mēs iegūstam 2 vienādojumus - vienu no s koeficientiem un otro no pārējiem:
( a + b ) s + 3 a -2 b = 3
a + b = 0, 3 a -2 b = 3
a = 3/5, b = -3/5
F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)
Tagad F (s) var viegli pārveidot, izmantojot eksponenta funkcijas pārveidojumu tabulu:
f ( t ) = (3/5) e 2 t - (3/5) e -3 t
Skatīt arī
KALKULS
- Ierobežot
- Atvasinājums
- Neatņemama
- Sērija
- Laplasa transformācija
- Konversija
- Rēķina simboli
ĀTRAS TABULAS