Distribución de probabilidad
En probabilidad y estadística, la distribución es una característica de una variable aleatoria, describe la probabilidad de la variable aleatoria en cada valor.
Cada distribución tiene una determinada función de densidad de probabilidad y una función de distribución de probabilidad.
Aunque hay un número indefinido de distribuciones de probabilidad, hay varias distribuciones comunes en uso.
- Función de distribución acumulativa
- Tabla de distribuciones continuas
- Tabla de distribuciones discretas
Función de distribución acumulativa
La distribución de probabilidad se describe mediante la función de distribución acumulativa F (x),
que es la probabilidad de que la variable aleatoria X obtenga un valor menor o igual ax:
F ( x ) = P ( X ≤ x )
Distribución continua
La función de distribución acumulada F (x) se calcula mediante la integración de la función de densidad de probabilidad f (u) de la variable aleatoria continua X.
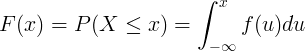
Distribución discreta
La función de distribución acumulada F (x) se calcula sumando la función de masa de probabilidad P (u) de la variable aleatoria discreta X.
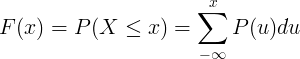
Tabla de distribuciones continuas
La distribución continua es la distribución de una variable aleatoria continua.
Ejemplo de distribución continua
...
Tabla de distribuciones continuas
| Nombre de distribución | Símbolo de distribución | Función de densidad de probabilidad (pdf) | Media | Diferencia |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| Normal / gaussiano | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| Uniforme | X ~ U ( a , b ) |
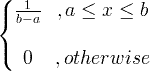 |
|
|
| Exponencial | X ~ exp (λ) | |
|
|
| Gama | X ~ gamma ( c , λ) | 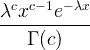 x / 0, c / 0, λ/ 0 |
|
|
| Chi cuadrado | X ~ χ 2 ( k ) |
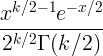 |
k |
2 k |
| Wishart | ||||
| F | X ~ F ( k 1 , k 2 ) |
|||
| Beta | ||||
| Weibull | ||||
| Logaritmo normal | X ~ LN (μ, σ 2 ) |
|||
| Rayleigh | ||||
| Cauchy | ||||
| Dirichlet | ||||
| Laplace | ||||
| Exacción | ||||
| Arroz | ||||
| T de estudiante |
Tabla de distribuciones discretas
La distribución discreta es la distribución de una variable aleatoria discreta.
Ejemplo de distribución discreta
...
Tabla de distribuciones discretas
| Nombre de distribución | Símbolo de distribución | Función de masa de probabilidad (pmf) | Media | Diferencia | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| Binomio | X ~ Bin ( n , p ) |
|
np |
np (1- p ) |
|
| Poisson | X ~ Poisson (λ) |
|
λ ≥ 0 |
λ |
λ |
| Uniforme | X ~ U ( a, b ) |
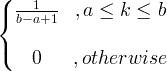 |
|
|
|
| Geométrico | X ~ Geom ( p ) |
|
|
|
|
| Hipergeométrico | X ~ HG ( N , K , n ) |
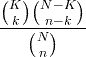 |
N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N |
|
|
| Bernoulli | X ~ Berna ( p ) |
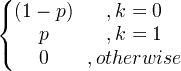 |
p |
p (1- p ) |
|
Ver también
PROBABILIDAD Y ESTADISTICAS
- Probabilidad básica
- Expectativa
- Diferencia
- Desviación Estándar
- Distribución de probabilidad
- Distribución normal
- Símbolos estadísticos
MESAS RÁPIDAS