Desviación Estándar

En probabilidad y estadística, la desviación estándar de una variable aleatoria es la distancia promedio de una variable aleatoria del valor medio.

Representa cómo se distribuye la variable aleatoria cerca del valor medio. Una pequeña desviación estándar indica que la variable aleatoria se distribuye cerca del valor medio. La desviación estándar grande indica que la variable aleatoria se distribuye lejos del valor medio.

Fórmula de definición de desviación estándar

La desviación estándar es la raíz cuadrada de la varianza de la variable aleatoria X, con un valor medio de μ.

\ sigma = estándar (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

De la definición de la desviación estándar podemos obtener

\ sigma = estándar (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Desviación estándar de variable aleatoria continua

Para una variable aleatoria continua con valor medio μ y función de densidad de probabilidad f (x):

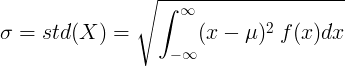
\ sigma = estándar (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

o

\ sigma = std (X) = \ sqrt {\ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}

Desviación estándar de variable aleatoria discreta

Para la variable aleatoria discreta X con valor medio μ y función de masa de probabilidad P (x):

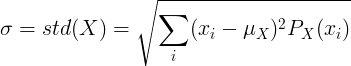
\ sigma = estándar (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

o

\ sigma = std (X) = \ sqrt {\ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2}

 

Distribución de probabilidad ►

 

Ver también

PROBABILIDAD Y ESTADISTICAS
MESAS RÁPIDAS