Función arcoseno
arcsin (x), sin -1 (x), función de seno inverso .
Definición arcsin
El arcoseno de x se define como la función de seno inverso de x cuando -1≤x≤1.
Cuando el seno de y es igual ax:
sin y = x
Entonces el arcoseno de x es igual a la función de seno inverso de x, que es igual ay:
arcosen x = sin -1 x = y
Ejemplo
arcosen 1 = sin -1 1 = π / 2 rad = 90 °
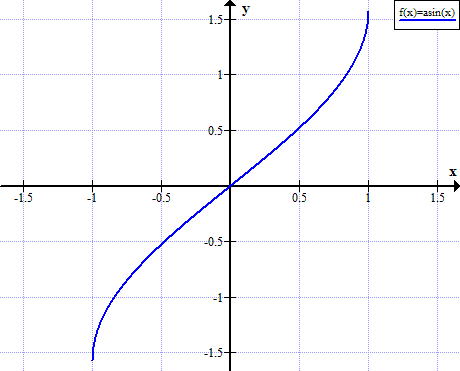
Gráfico de arcosen
Reglas de Arcsin
| Nombre de la regla | Regla |
|---|---|
| Seno de arcoseno | sin (arcosen x ) = x |
| Arcoseno de seno | arcsin (sin x ) = x +2 k π, cuando k ∈ℤ ( k es un número entero) |
| Arco de argumento negativo | arcosen (- x ) = - arcosen x |
| Ángulos complementarios | arcosen x = π / 2 - arcos x = 90 ° - arcos x |
| Suma de arcos | arcsin α + arcsin ( β ) = arcsin ( α√ (1- β 2 ) + β√ (1- α 2 ) ) |
| Diferencia de arco | arcsin α - arcsin ( β ) = arcsin ( α√ (1- β 2 ) - β√ (1- α 2 ) ) |
| Coseno de arcoseno | |
| Tangente de arcoseno | |
| Derivada de arcoseno | 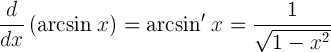 |
| Integral indefinida de arcoseno |
Mesa Arcsin
| x | arcosen (x) (rad) |
arcosen (x) (°) |
|---|---|---|
| -1 | -π / 2 | -90 ° |
| -√ 3 /2 | -π / 3 | -60 ° |
| -√ 2 /2 | -π / 4 | -45 ° |
| -1/2 | -π / 6 | -30 ° |
| 0 | 0 | 0 ° |
| 1/2 | π / 6 | 30 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 3 | 60 ° |
| 1 | π / 2 | 90 ° |
Ver también
- Función seno
- Función arcoseno
- Función Arctan
- Calculadora de arcsin
- Conversor de grados a radianes
- Arcosin de 0
- Arcosin de 1
- Arco del infinito
- Gráfico de arco
- Derivado de arcsina
- Arcsin integral
- Pecado de arcsin
- Cos de arcsin
- Bronceado de arcsin