फिबोनाची क्रमांक आणि क्रम

फिबोनॅकी अनुक्रम संख्यांचा क्रम आहे, जेथे प्रत्येक संख्या 0 आणि 1 असलेल्या पहिल्या दोन संख्या वगळता 2 मागील अंकांची बेरीज आहे.

• फिबोनाची क्रम सूत्र
• गोल्डन रेशियो कन्व्हर्जन
• फिबोनाची क्रम सारणी
• फिबोनाकी सीक्वेन्स कॅल्क्युलेटर
• फिबोनॅकी फंक्शनचा सी ++ कोड

फिबोनाची क्रम सूत्र

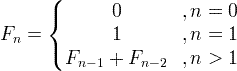
उदाहरणार्थ:

एफ ₀ = 0

एफ ₁ = 1

एफ ₂ = एफ ₁ + एफ ₀ = 1 + 0 = 1

एफ ₃ = एफ ₂ + एफ ₁ = 1 + 1 = 2

एफ ₄ = एफ ₃ + एफ ₂ = 2 + 1 = 3

एफ ₅ = एफ ₄ + एफ ₃ = 3 + 2 = 5

...

गोल्डन रेशियो कन्व्हर्जन

दोन अनुक्रमिक फिबोनाची संख्येचे गुणोत्तर, सुवर्ण प्रमाणात रुपांतर करते:

φ हा सुवर्ण गुणोत्तर = (1 + √ 5 ) / 2 ≈ 1.61803399 आहे

फिबोनाची क्रम सारणी

एन	एफ एन
0	0
1	1
2	1
3 |	2
4	3 |
5	5
6	8
7	13
8	21
9	34
10	55
11	89
12	144
13	233
14	377
15	610
16	987
17	1597
18	2584
19	4181
20	6765

फिबोनाकी सीक्वेन्स कॅल्क्युलेटर

टीबीडी

फिबोनाची फंक्शनचा सी कोड

double Fibonacci(unsigned int n)

{

    double f_n =n;

    double f_n1=0.0;

    double f_n2=1.0;

 

    if( n / 1 ) {

        for(int k=2; k<=n; k++) {

            f_n  = f_n1 + f_n2;

            f_n2 = f_n1;

            f_n1 = f_n;

        }

    }

 

    return f_n;

}