शून्य क्रमांक (0)
शून्य संख्या व्याख्या
शून्य एक संख्या आहे ज्याचा वापर गणितामध्ये कोणतेही प्रमाण किंवा शून्य प्रमाणात नाही.
जेव्हा टेबलवर 2 सफरचंद असतात आणि आम्ही 2 सफरचंद घेतो तेव्हा असे म्हणू शकतो की टेबलवर शून्य सफरचंद आहेत.
शून्य संख्या सकारात्मक संख्या नाही आणि नकारात्मक संख्या नाही.
शून्य हा इतर क्रमांकाचा प्लेसहोल्डर अंक देखील आहे (उदा: 40,103, 170)
शून्य एक संख्या आहे?
शून्य एक संख्या आहे. ती सकारात्मक किंवा नकारात्मक संख्या नाही.
शून्य अंक
नंबर लिहिताना प्लेसहोल्डर म्हणून शून्य अंक वापरला जातो.
उदाहरणार्थ:
204 = 2 × 100 + 0 × 10 + 4 × 1
शून्य क्रमांक इतिहास
शून्य क्रमांकाचा शोध कोणी लावला?
आधुनिक 0 चिन्हाचा शोध 6 व्या शतकात भारतात लागला होता, नंतर पर्शियन आणि अरबांनी आणि नंतर युरोपमध्ये वापरला.
शून्याचे प्रतीक
शून्य संख्या 0 चिन्हासह दर्शविली जाते .
अरबी अंक प्रणाली ٠ प्रतीक वापरते.
शून्य संख्या गुणधर्म
x कोणत्याही संख्येचे प्रतिनिधित्व करते.
| ऑपरेशन | नियम | उदाहरण |
|---|---|---|
या व्यतिरिक्त |
x + 0 = x |
3 + 0 = 3 |
वजाबाकी |
x - 0 = x |
3 - 0 = 3 |
गुणाकार |
x × 0 = 0 |
5 × 0 = 0 |
विभागणी |
0 ÷ x = 0 , जेव्हा x ≠ 0 |
0 ÷ 5 = 0 |
| x ÷ 0 अपरिभाषित आहे |
5 ÷ 0 अपरिभाषित आहे |
|
क्षोभ |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
मूळ |
√ 0 = 0 |
|
लोगारिदम |
लॉग बी (0) अपरिभाषित आहे |
|
| |
||
फॅक्टोरियल |
0! = 1 |
|
साईन |
sin 0º = 0 |
|
कोझिन |
कॉस 0º = 1 |
|
स्पर्शिका |
टॅन 0º = 0 |
|
व्युत्पन्न |
0 '= 0 |
|
अखंड |
∫ 0 डी x = 0 + से |
|
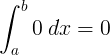 |
शून्य व्यतिरिक्त
संख्येचे शून्य शून्य जोडणे समान आहे:
x + 0 = x
उदाहरणार्थ:
5 + 0 = 5
शून्य वजाबाकी
शून्य शून्य शून्यचे वजाबाकी संख्येइतकी असते:
x - 0 = x
उदाहरणार्थ:
5 - 0 = 5
शून्याने गुणाकार
शून्याच्या संख्येचे गुणाकार शून्य बरोबर आहे:
x × 0 = 0
उदाहरणार्थ:
5 × 0 = 0
शून्याने विभाजित केलेली संख्या
शून्याद्वारे संख्येचे विभागणी परिभाषित केलेले नाही:
x ÷ 0 अपरिभाषित आहे
उदाहरणार्थ:
5 ÷ 0 अपरिभाषित आहे
शून्यावर एका संख्येने विभाजित केले
एका संख्येद्वारे शून्याचे विभाजन शून्य आहे:
0 ÷ x = 0
उदाहरणार्थ:
0 ÷ 5 = 0
शून्य उर्जेची संख्या
शून्याने वाढवलेल्या संख्येची शक्ती एक आहे:
x 0 = 1
उदाहरणार्थ:
5 0 = 1
शून्य लोगो
शून्याचा बेस बी लोगारिदम अपरिभाषित आहे:
लॉग बी (0) अपरिभाषित आहे
शून्य मिळविण्यासाठी आम्ही बेस बी वाढवू शकतो अशी कोणतीही संख्या नाही.
जेव्हा x शून्य रूपांतरित करते तेव्हा x च्या बेस बी लोगारिदमची मर्यादा वजा अनंत असते:
![]()
शून्य असलेले सेट
शून्य ही नैसर्गिक संख्या, पूर्णांक संख्या, वास्तविक संख्या आणि गुंतागुंतीच्या संख्येच्या संचाचा एक घटक आहे:
| सेट | सदस्यता चिन्ह सेट करा |
|---|---|
| नैसर्गिक संख्या (नकारात्मक नाही) | 0 ∈ ℕ 0 |
| पूर्णांक संख्या | 0 ∈ ℤ |
| वास्तविक संख्या | 0 ∈ ℝ |
| जटिल संख्या | 0 ∈ ℂ |
| तर्कसंगत क्रमांक | 0 ∈ ℚ |
शून्य सम किंवा विषम संख्या आहे?
सम संख्यांचा संच असा आहे:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
विषम संख्यांचा संच आहे:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
शून्य हे पूर्णांक 2 चे पूर्णांक आहे:
0 × 2 = 0
झिरो सेट केलेल्या सम संख्याचे एक सदस्य आहे:
0 ∈ {2 के , के ∈ℤ}
तर शून्य एक सम संख्या आहे आणि एक विचित्र संख्या नाही.
शून्य एक नैसर्गिक संख्या आहे?
सेट केलेल्या नैसर्गिक संख्येसाठी दोन परिभाषा आहेत.
नकारात्मक नकारात्मक पूर्णांकांचा संच:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
सकारात्मक पूर्णांकाचा संच:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
शून्य नकारात्मक नकारात्मक पूर्णांकांच्या संचाचा सदस्य आहे:
0 ∈ ℕ 0
शून्य सकारात्मक पूर्णांकाच्या संचाचा सदस्य नाहीः
0 ∉ ℕ 1
पूर्ण संख्या शून्य आहे?
संपूर्ण संख्येसाठी तीन व्याख्या आहेत:
पूर्णांक संख्यांचा संच:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
नकारात्मक नकारात्मक पूर्णांकांचा संच:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
सकारात्मक पूर्णांकाचा संच:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
शून्य पूर्णांक संख्या आणि नकारात्मक नकारात्मक पूर्णांकांच्या संचाचा एक सदस्य आहे:
0 ∈ ℤ
0 ∈ ℕ 0
शून्य सकारात्मक पूर्णांकाच्या संचाचा सदस्य नाहीः
0 ∉ ℕ 1
शून्य पूर्णांक संख्या आहे का?
पूर्णांक संख्यांचा संच:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
शून्य पूर्णांक संख्यांच्या संचाचा सदस्य आहे:
0 ∈ ℤ
शून्य एक पूर्णांक संख्या आहे.
शून्य एक तर्कसंगत संख्या आहे?
तर्कसंगत क्रमांक एक अशी संख्या आहे जी दोन पूर्णांक संख्येचा भाग म्हणून व्यक्त केली जाऊ शकते:
ℚ = { n / मी ; एन , मी ∈ℤ}
दोन पूर्णांक संख्येचा भाग म्हणून शून्य लिहिले जाऊ शकते.
उदाहरणार्थ:
0 = 0/3
तर शून्य एक तर्कसंगत संख्या आहे.
शून्य एक सकारात्मक संख्या आहे का?
शून्यापेक्षा मोठी संख्या म्हणून सकारात्मक संख्या परिभाषित केली जाते:
x / 0
उदाहरणार्थ:
5/ 0
शून्य शून्यापेक्षा जास्त नसल्यामुळे ती सकारात्मक संख्या नाही.
शून्य एक प्राथमिक संख्या आहे?
संख्या 0 ही प्राथमिक संख्या नाही.
शून्य ही एक सकारात्मक संख्या नाही आणि त्यात विवाहाची संख्या असीम आहे.
सर्वात कमी संख्या 2 आहे.